9

I am playing around with using Tube as an option under PlotStyle for a ParametricPlot3D curve, with the end-goal of exporting the model to .stl in order to 3D print it. Overall, it's working quite well, but I am consistently getting poor discretization of the tube along its azimuthal direction.

Here is one minimal example

ParametricPlot3D[
 {Cos[ωt], Sin[ωt], 0}
 , {ωt, 0, π/2}
 , ImageSize -> 500
 , SphericalRegion -> True
 , PlotRange -> All
 , PlotStyle -> Tube[0.2]
 ]

which produces the following output,

which is much more clearly a discrete 12-gon prism than a cylinder.

What control options do I have to improve the discretization along this dimension?

user21
  • 39,710
  • 8
  • 110
  • 167
Emilio Pisanty
  • 10,255
  • 1
  • 36
  • 69
  • 2
    ParametricPlot3D[{Cos[\[Omega]t], Sin[\[Omega]t], 0} , {\[Omega]t, 0, \[Pi]/2} , ImageSize -> 500 , SphericalRegion -> True , PlotRange -> All , PlotStyle -> Directive[CapForm["Square"]] ] /. Line -> (Tube[#, 0.2] &) – Syed Mar 27 '22 at 19:47
  • Further modify as you see fit: DiscretizeGraphics[p1, MaxCellMeasure -> {"Area" -> 0.002}] – Syed Mar 27 '22 at 20:00
  • @Syed Thanks, both are quite helpful. I will experiment a bit. I am reluctant to use the ReplaceAll Line→Tube method since once I export my model the resulting .stl comes out with missing wedges. (I'll try to produce a MWE and post it here in the next couple of days.) But hopefully there's some happy middle there. – Emilio Pisanty Mar 27 '22 at 20:10
  • If you could please load an image of what a "wedge" looks like, I would learn from it. Try Mesh->20 in the plot or experiment to find if it improves anything. Good luck. – Syed Mar 27 '22 at 20:14
  • @Syed By "wedge" I mean the choppy changes in direction in here. Once the layering is generated, a cross-section looks like this, with clear gaps in the model. – Emilio Pisanty Mar 27 '22 at 20:25
  • The problem seems to be downstream of ParametricPlot3D -- running Syed's code and exporting an STL produces nice connected tris. If you convert many connected-but-not-symbolically Lines to Tubes, then you'll get the wedges in your imgur links. – Adam Mar 27 '22 at 21:36

2 Answers2

7

This may be on site already, but I didn't find a good match. It's now in the docs for Tube, without the CapForm:

ParametricPlot3D[{Cos[ωt], Sin[ωt], 0}, {ωt, 
   0, π/2}, SphericalRegion -> True, PlotRange -> All, 
  Method -> {"TubePoints" -> 30}] /. 
 Line[pts_, rest___] :> {CapForm["Butt"], Tube[pts, 0.2, rest]}

enter image description here

Michael E2
  • 235,386
  • 17
  • 334
  • 747
7

Borrowed Stolen Adapted from @J.M., Extruding along a path, to add end caps to make a closed polyhedron for 3D printing:

(*Pixar method;http://jcgt.org/published/0006/01/01/*)
orthogonalDirections[{p1_?VectorQ, p2_?VectorQ}] := 
 Module[{s, w, w1, xx, yy, zz}, {xx, yy, zz} = Normalize[p2 - p1];
  s = 2 UnitStep[zz] - 1; w = -1/(s + zz); w1 = xx yy w;
  {{1 + s w xx^2, s w1, -s xx}, {w1, s + w yy^2, -yy}}]

orthogonalDirections[{p1_?VectorQ, p2_?VectorQ, p3_?VectorQ}] := 
 Module[{d, u, v}, {u, v} = Normalize /@ {p3 - p2, p1 - p2};
  If[Chop[Norm[u - v] Norm[u + v]] != 0, d = (u + v)/2; 
   Normalize /@ {d, Cross[u, d]}, orthogonalDirections[{p1, p2}]]]


extend[cs_, q_, d_, nrms_] := 
 cs + Outer[Times, 
   First[
    LinearSolve[Transpose[Prepend[-nrms, d]], q - Transpose[cs]]], d]


(for custom cross-sections)
crossSection[pointList_?MatrixQ, r_, csList_?MatrixQ] := 
 Module[{p1, p2}, {p1, p2} = Take[pointList, 2];
   (p1 + #) & /@ (r csList . orthogonalDirections[{p1, p2}])] /; 
  Last[Dimensions[pointList]] == 3 && Last[Dimensions[csList]] == 2


(for circular cross-sections)
crossSection[pointList_?MatrixQ, r_, n_Integer] := 
 crossSection[pointList, r, 
  Composition[Through, {Cos, Sin}] /@ Range[0, 2 Pi, 2 Pi/n]]


(approximate vertex normals,for a smooth appearance)
vertNormals[vl_ /; ArrayQ[vl, 3, NumericQ]] := 
 Block[{mdu, mdv, msh}, 
  msh = ArrayPad[#, {{1, 1}, {1, 1}}, "Extrapolated", 
      InterpolationOrder -> 2] & /@ Transpose[vl, {2, 3, 1}];
  mdu = ListCorrelate[{{1, 0, -1}}/2, #, {{-2, 1}, {2, -1}}, 0] & /@ 
    msh;
  mdv = ListCorrelate[{{-1}, {0}, {1}}/2, #, {{1, -2}, {-1, 2}}, 
      0] & /@ msh;
  MapThread[Composition[Normalize, Cross], 
   Transpose[{mdu, mdv}, {1, 4, 2, 3}], 2]]


MakePolygons // ClearAll;
MakePolygons[vl_ /; ArrayQ[vl, 3, NumericQ], 
  OptionsPattern[{"Normals" -> True, "Closed" -> False}]] := 
 Module[{dims = Most[Dimensions[vl]]}, GraphicsComplex[Apply[Join, vl],
   {If[TrueQ@OptionValue@"Closed",
     Polygon[{Range@Length@First@vl, 
       Range[1 + Length@First@vl (Length@vl - 1), 
        Length@First@vl*Length@vl]}, VertexNormals -> None],
     {}],
    Polygon[
     Flatten[
      Apply[Join[Reverse[#1], #2] &, 
       Partition[
        Partition[Range[Times @@ dims], Last[dims]], {2, 2}, {1, 
         1}], {2}], 1]]}, 
   If[TrueQ[OptionValue["Normals"] /. Automatic -> True], 
    VertexNormals -> Apply[Join, vertNormals[vl]], Unevaluated[]]]]


TubePolygons // ClearAll; 
TubePolygons // Options = {"Normals" -> True, "Scale" -> 1., 
  "Closed" -> False};
TubePolygons[path_?MatrixQ, cs : (_Integer | _?MatrixQ), 
  OptionsPattern[]] := 
 With[{p3 = PadRight[path, {Automatic, 3}]}, 
  MakePolygons[
   FoldList[
    Function[{p, t}, 
     extend[p, t[[2]], t[[2]] - t[[1]], orthogonalDirections[t]]], 
    crossSection[p3, OptionValue["Scale"], cs], 
    Partition[p3, 3, 1, {1, 2}, {}]], 
   "Normals" -> OptionValue["Normals"], 
   "Closed" -> OptionValue["Closed"]]]

OP's example:

path = First@
   Cases[
    ParametricPlot3D[{Cos[ωt], Sin[ωt], 0}, {ωt, 
      0, π/2}, ImageSize -> 500, SphericalRegion -> True, 
     PlotRange -> All], Line[l_] :> l, Infinity];

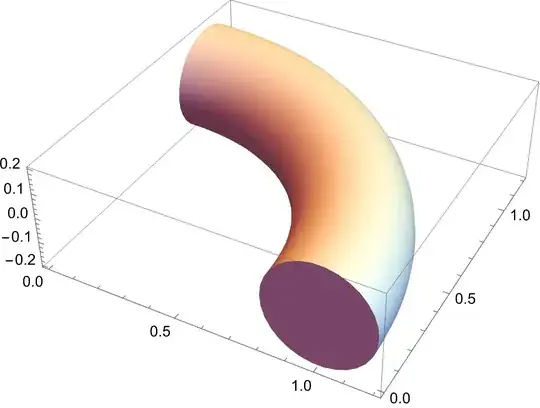
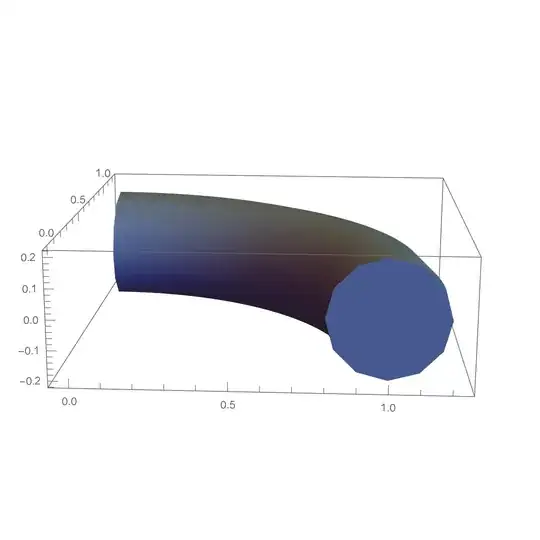
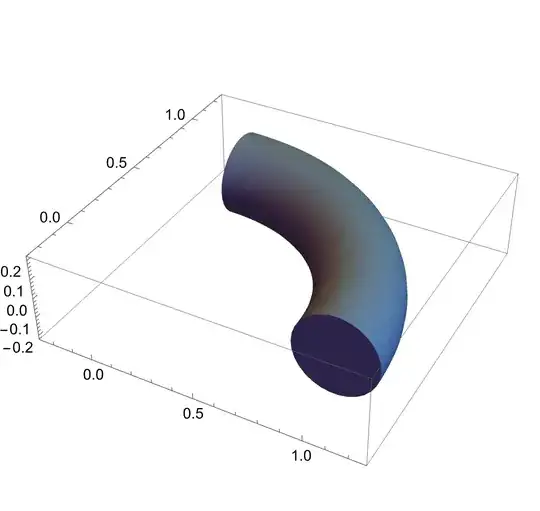
Graphics3D[{EdgeForm[], 
  TubePolygons[path, 30, "Normals" -> True, "Scale" -> 0.2, 
   "Closed" -> True]}, Axes -> True]

enter image description here

Michael E2
  • 235,386
  • 17
  • 334
  • 747