I wish to solve the following system of equations:
$\frac{d^2f}{dr^2}- \frac{1}{r} \frac{df}{dr} = 2 f(r)\phi(r)^2$
$\frac{d^2\phi}{dr^2} + \frac{1}{r}\frac{d\phi}{dr} = \frac{1}{r^2} f(r)^2\phi(r) + \phi(r)(\phi(r)^2-1) - \frac{2\alpha}{\xi} a(r)\phi(r) + \frac{\sqrt{2}}{e^2 \xi } a(r)^2 \phi(r)$
$\frac{1}{r}\frac{da}{dr} + \frac{d^2 a}{dr^2} = 2 a(r) \phi^2(r) + \sqrt{2} \alpha e^2 (1-\phi^2(r) + 2 \frac{\alpha}{\xi} a(r))$
with the boundary conditions:
$\phi(0) = 0 , \phi(\infty) = 1$
$f(0)=1,f(\infty) = 0$
$a(0)=a_0,a(\infty)=0$
These are vortex solutions of a certain kind and I wish to solve these equations given any parameters $\alpha,e,\xi$. The value of $a_0$ needs to be picked, for each choice of $\alpha,e,\xi$, such that the Hamiltonian functional is minimised, which is given by:
$H = \int du \Big[\frac{\xi}{\sqrt{2}}\frac{1}{u}\Big(\frac{df}{du}\Big)^2 + \sqrt{2}\xi \Big\{u \Big(\frac{df}{du}\Big)^2 + \frac{1}{u}\phi^2(u)f^2(u)\Big\}+\frac{\xi}{\sqrt{2}}u (\phi^2(u)-1)^2 + u \frac{1}{e^2}\Big(\frac{da}{du}\Big)^2 + u \frac{2}{e^2} a^2(u)\phi^2(u) + 2\sqrt{2} \alpha a(u)u(1-\phi^2(u)) + u\frac{2\sqrt{2}\alpha^2a^2(u)}{\xi}\Big]$
I tried the following : 1. perform a frobenius expansion close to the origin and find the first few coefficients. They can be written as a function of three unknowns $f_2,\phi_1,a_0$.
f[f2_, \[Phi]1_, a0_, e_, \[Xi]_, \[Alpha]_, r_] :=
1 + f2 r^2 + \[Phi]1^2/
4 r^4 + (-e^2 \[Xi] \[Phi]1^2 -
2 \[Alpha] e^2 a0 \[Phi]1^2 + Sqrt[2] a0^2 \[Phi]1^2 +
6 e^2 \[Xi] f2 \[Phi]1^2 )/(48 e^2 \[Xi]) r^6
\[Phi][f2_, \[Phi]1_, a0_, e_, \[Xi]_, \[Alpha]_,
r_] := \[Phi]1 r + (-e^2 \[Xi] \[Phi]1 -
2 \[Alpha] e^2 a0 \[Phi]1 + Sqrt
[2] a0^2 \[Phi]1 +
2 e^2 \[Xi] f2 \[Phi]1)/(8 e^2 \[Xi]) r^3
a[f2_, \[Phi]1_, a0_, e_, \[Xi]_, \[Alpha]_, r_] :=
a0 + (Sqrt[2] \[Alpha] e^2 \[Xi] +
2 Sqrt[2] \[Alpha]^2 e^2 a0 )/(4 \[Xi]) r^2 + \
(\[Alpha]^3 e^4 \[Xi] + 2 \[Alpha]^4 e^4 a0 -
Sqrt[2] \[Alpha] e^2 \[Xi]^2 \[Phi]1^2 +
2 \[Xi]^2 a0 \[Phi]1^2)/(16 \[Xi]^2) r^4
- The derivatives of these expansions are given by:
df[f2_, \[Phi]1_, a0_, e_, \[Xi]_, \[Alpha]_, r_] :=
2 f2 r + \[Phi]1^2 r^3
d\[Phi][f2_, \[Phi]1_, a0_, e_, \[Xi]_, \[Alpha]_, r_] := \[Phi]1 +
3 (-e^2 \[Xi] \[Phi]1 - 2 \[Alpha] e^2 a0 \[Phi]1 + Sqrt
[2] a0^2 \[Phi]1 +
2 e^2 \[Xi] f2 \[Phi]1)/(8 e^2 \[Xi]) r^2
da[f2_, \[Phi]1_, a0_, e_, \[Xi]_, \[Alpha]_,
r_] := (Sqrt[2] \[Alpha] e^2 \[Xi] +
2 Sqrt[2] \[Alpha]^2 e^2 a0 )/(2 \[Xi]) r + \
(\[Alpha]^3 e^4 \[Xi] + 2 \[Alpha]^4 e^4 a0 -
Sqrt[2] \[Alpha] e^2 \[Xi]^2 \[Phi]1^2 +
2 \[Xi]^2 a0 \[Phi]1^2)/(4 \[Xi]^2) r^3
- and then use them as initial conditions for ParametricNDSolve
soln = ParametricNDSolve[{r f''[r] - f'[r] - 2 r f[r] \[Phi][r]^2 ==
0 , r^2 \[Phi]''[r] + r \[Phi]'[r] - f[r]^2 \[Phi][r] -
r^2 \[Phi][r]^3 + r^2 \[Phi][r] +
2 (\[Alpha]/\[Xi]) a[r] \[Phi][r] r^2 -
r^2 (Sqrt[2]/(e^2 \[Xi])) a[r]^2 \[Phi][r] == 0,
a'[r] + r a''[r] - 2 r a[r] \[Phi][r]^2 -
Sqrt[2] \[Alpha] e^2 r (1 - \[Phi][r]^2 +
2 (\[Alpha]/\[Xi]) a[r]) == 0,
f[0.1] ==
f[f2, \[Phi]1, a0, e, \[Xi], \[Alpha], 0.1], \[Phi][
0.1] == \[Phi][f2, \[Phi]1, a0, e, \[Xi], \[Alpha], 0.1],
a[0.1] == a[f2, \[Phi]1, a0, e, \[Xi], \[Alpha], 0.1],
f'[0.1] ==
df[f2, \[Phi]1, a0, e, \[Xi], \[Alpha], 0.1], \[Phi]'[0.1] ==
d\[Phi][f2, \[Phi]1, a0, e, \[Xi], \[Alpha], 0.1],
a'[0.1] == da[f2, \[Phi]1, a0, e, \[Xi], \[Alpha], 0.1]}, {\[Phi],
f, a}, {r, 0.1, 10}, {f2, \[Phi]1, a0, e, \[Xi], \[Alpha]}]
My intention was to then vary $f_2,\phi_1,a_0$ so as to match the bcs at $\infty$. I was successful for the case with $\alpha=0$. For example with $e=3,\xi=1$, I get the following
Plot[Evaluate[
Table[f[-0.5, p1, 0, 3, 1, 0][r], {p1, 0.85317102502, 0.85317102503,
0.000000000001}] /. soln], {r, 0.1, 10},
PlotRange -> {-0.05, 1.1}]
Here $f_2 = -0.5,a_0=0,e=3,\xi=1,\alpha=0$ and the graph I get for $f$ by varying through parameter $\phi_1$ so as to match boundary conditions at infinity is :
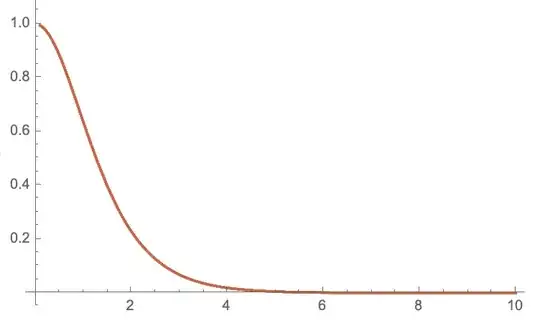
However, things get complicated if $\alpha \neq 0$, something like $\alpha = 10$, as then I would have to vary three parameters $f_2,\phi_1,a_0$ simultaneously while also checking whether the Hamiltonian is minimized which is making things very awkward.
My question would be what efficient approach should I be taking to solve such system of equations with stiff boundary conditions while also keeping in mind the value of $a_0$ which is unfixed as far as physical boundary conditions are concerned.
EDIT:
f1[r] = f[-0.5, 0.85317102502, 0, 3, 1, 0][r] /. soln
df1[r] = f[-0.5, 0.85317102502, 0, 3, 1, 0]'[r] /. soln
\[Phi]1[r] = \[Phi][-0.5, 0.85317102502, 0, 3, 1, 0][r] /. soln
d\[Phi]1[r] = \[Phi][-0.5, 0.85317102502, 0, 3, 1, 0]'[r] /. soln
a1[r] = a[-0.5, 0.85317102502, 0, 3, 1, 0][r] /. soln
da1[r] = a[-0.5, 0.85317102502, 0, 3, 1, 0]'[r] /. soln
e1 = 3; \[Alpha]1 = 0; \[Xi]1 = 1;
H[r_] := \[Xi]1/Sqrt[2] (1/r) df1[r]^2 +
Sqrt[2] \[Xi]1 (r d\[Phi]1[r]^2 + (1/r) \[Phi]1[r]^2 f1[
r]^2 ) + \[Xi]1/Sqrt[2] r (\[Phi]1[r]^2 - 1)^2 +
r (1/e1^2) da1[r]^2 + r (2/e1^2) a1[r]^2 \[Phi]1[r]^2 +
2 Sqrt[2] \[Alpha]1 a1[r] r (1 - \[Phi]1[r]^2) +
2 Sqrt[2] r \[Alpha]1^2 a1[r]^2/\[Xi]1
E1 = NIntegrate[H[r], {r, 0.1, 5}]
The graph for $\phi$ is accurate only till $r=5$, hence the integral is performed only till 5. This is one of the drawbacks of this approach. It is not stable and consistent enough to give accurate answers.
EDIT2: Just solving the above equations with a given value of $a_0$ would also be helpful without the minimization. I can perform the latter step later by scanning over the possible parameter space for $a_0$. I tried doing this using the inbuilt FEM in Mathematica v12 but I was getting kinks and wiggles in the graphs which again are not useful since I'm calculating derivatives as well.
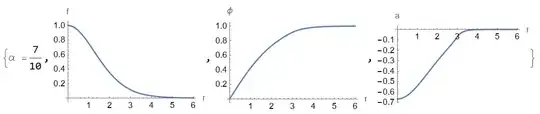
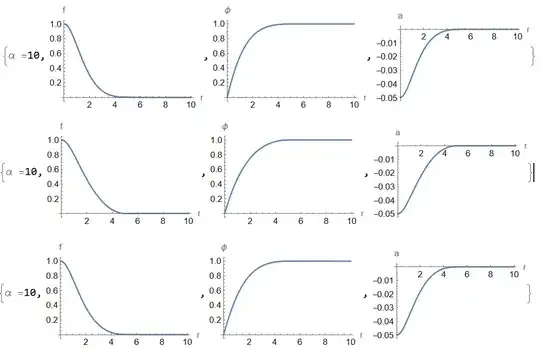

E1positive or negative? Could we minimizeE1^2? – Alex Trounev Apr 05 '22 at 03:10