5

The vectors given in problem are:

p1 = {1, 2, 2}; 
p2 = {3, 1, 1/4}; 
p3 = {2, 3, 9/4}; 
p4 = {5, 2, 0}; 
p5 = {3/2, 5/4, 19/16};

Find all 5 of the (internal) angles of S. Note that the internal angles of an n-sided polygon always add up to . Give the angles in degrees in numerical value.

I tried VectorAngle[p3 - p1, p5 - p1] 3*Pi // N I don't think the answer is correct.

Alexey Popkov
  • 61,809
  • 7
  • 149
  • 368
MJY
  • 51
  • 1

2 Answers2

5
p1 = {1, 2, 2};
p2 = {3, 1, 1/4};
p3 = {2, 3, 9/4};
p4 = {5, 2, 0};
p5 = {3/2, 5/4, 19/16};
pts = {p1, p2, p3, p4, p5}
chReg = ConvexHullRegion[pts]

angs = PolygonAngle[chReg]*180/\[Pi] // N

{104.946, 105.07, 141.61, 137.942, 50.4316}

Total[angs]

540.

Visualization:

Graphics3D[{
  EdgeForm[Black]
  , Black
  , Line@pts
  , AbsolutePointSize[10]
  , Red, Point@pts
  , LightRed, chReg
  }
 , Boxed -> True
 ]

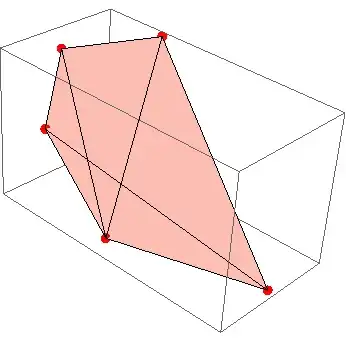
enter image description here

Syed
  • 52,495
  • 4
  • 30
  • 85
4

This is an extended comment, because I am a bit confused.

In the OP the following is given:

p1 = {1, 2, 2};
p2 = {3, 1, 1/4};
p3 = {2, 3, 9/4};
p4 = {5, 2, 0};
p5 = {3/2, 5/4, 19/16};

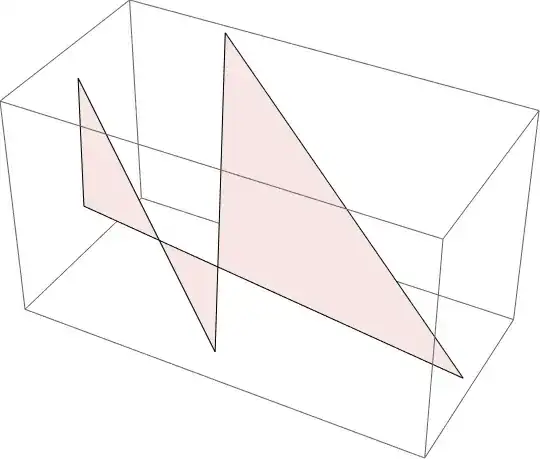
from which we can create a Polygon

poly = Polygon[{p1, p2, p3, p4, p5}];

Graphics3D[poly]

polygon

From the above picture, I count $9$ internal angles. Based on this table the sum of angles of the Nonagon is equal to $1260$. Which can be easily derived using PolygonAngle in the following manner:

FullSimplify@Total@PolygonAngle[poly] /. Pi -> 180 Degree

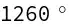
totalangles

bmf
  • 15,157
  • 2
  • 26
  • 63
  • 2
    It is strange that SimplePolygonQ@poly returns True because poly is a self-intersecting polygon: Graphics3D[{poly, Red, Sphere[#, .1] & /@ {p1, p2, p3, p4, p5}}]. – Alexey Popkov Apr 07 '22 at 05:40
  • 2
    A proof: {RegionIntersection[Line[{p1, p2}], Line[{p4, p5}]], RegionIntersection[Line[{p2, p3}], Line[{p4, p5}]]}. – Alexey Popkov Apr 07 '22 at 06:23
  • @AlexeyPopkov thanks for bringing this up. I did not check it myself. That's strange indeed. – bmf Apr 07 '22 at 15:22
  • 1
    Wolfram support confirmed that it is a known bug in SimplePolygonQ ([CASE:4930736]). – Alexey Popkov Apr 08 '22 at 02:11
  • @AlexeyPopkov many thanks again for this. Do you want to write an answer? Should I just update the existing answer? Nothing is required? Not sure to be honest – bmf Apr 08 '22 at 02:12
  • The OP's question isn't well-posed because it doesn't make it clear which polygon is under consideration. You can simply update your answer with this information. It is also interesting that PolygonAngle seemingly is able to handle self-intersection polygons in a special way (but I didn't check the correctness and how it does it). Or you may do nothing unless the OP updates the question. – Alexey Popkov Apr 08 '22 at 02:19