Finding the roots of Abs[Hypergeometric1F1[1/4 (3 - (2 x)/I), 1.5, I]]=0

Question

I want to solve for the first 100 or more zeros of Abs[Hypergeometric1F1[1/4 (3 - (2 x)/I), 1.5, I]]=0;

The following code is my simple attempt：

a = 2000;
Quiet@FindRoot[Abs[Hypergeometric1F1[1/4 (3 - (2*x)/I), 1.5, I]] == 0, {x, #, 0, a}] & /@ Range[a] //Values//Flatten//Round[#, 0.001]&//Sort//DeleteDuplicates

But I lose some roots when solving for more roots.

How can I precisely find more roots.

Answer 1

Approximating a function with a Chebyshev interpolation is a powerful way to find roots. See links at the beginning of the code dump. Best to use an analytic function with this method (i.e., drop Abs, which is not differentiable). Takes about 5 sec. to find cc and rts50.

cc = adaptiveChebSeries[
   x |-> Hypergeometric1F1[1/4 (3 - (2*x)/I), 15/10, I], 1, 20000, 
   "Points" -> 2^8, WorkingPrecision -> 50];
Length@cc
(*  130  *)
rts50 = chebRoots[cc, {1, 20000}];
Length@rts50
(*  63  *)
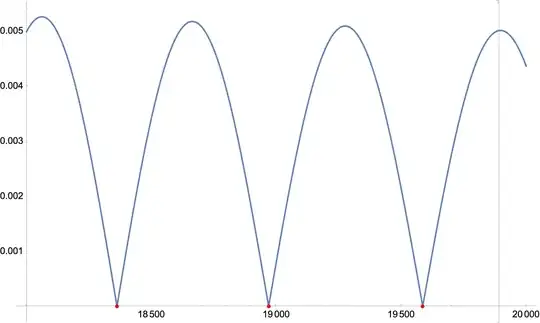
ReImPlot[
 Hypergeometric1F1[1/4 (3 - (2*x)/I), 15/10, I], {x, 1, 20000}, 
 Mesh -> {rts50}, MeshStyle -> Red, 
 ScalingFunctions -> {"Log", Automatic}]

Code dump

Code taken from my answer here; see my answer here for a discussion of the code.

(* Chebyshev extreme points *)
chx[n_, prec_: MachinePrecision] := N[Cos[Range[0, n]/n Pi], prec];
(* Chebyshev series approximation to f )
Clear[chebSeries];
chebSeries[f_, a_, b_, n_, prec_: MachinePrecision] := Module[{x, y, cc},
   x = Rescale[chx[n, prec], {-1, 1}, {a, b}];
   y = f /@ x;                       ( function values at Chebyshev points )
   cc = Sqrt[2/n] FourierDCT[y, 1];  ( get coeffs from values )
   cc[[{1, -1}]] /= 2;               ( adjust first & last coeffs *)
   cc
   ];
(* recursively double the Chebyshev points

until the PrecisionGoal is met
The function values are memoized in f0
*)

Clear[adaptiveChebSeries];
Options[adaptiveChebSeries] = {PrecisionGoal -> 14, "Points" -> 32, 
   WorkingPrecision -> MachinePrecision, MaxIterations -> 5};
adaptiveChebSeries[f_, a_, b_, OptionsPattern[]] := 
 Module[{cc, f0, max, len = 0, sum},
  f0[x_] := f0[x] = f[x];  (* values reused in subsequent series )
  NestWhile[
   (cc = chebSeries[f0, a, b, #, OptionValue[WorkingPrecision]];
     ( check error estimate )
     max = Max@Abs@cc;     ( sum the tail of the series )
     sum = 0;              ( relative to the max coefficient )
     len = LengthWhile[
       Reverse@cc, (sum += Abs@#) < 10^-OptionValue[PrecisionGoal]max &];
     2 #) &,               (* double the number of points )
   OptionValue["Points"],
   len < 3 && # <= 2^OptionValue[MaxIterations] OptionValue["Points"] &
                           ( at least two coefficients dropped *)
   ];
  If[len < 3, 
   Message[adaptiveChebSeries::cvmit, OptionValue[MaxIterations]]];
  If[TrueQ[len > 1], Drop[cc, 1 - len], cc]
  ]
(* "Chebyshev companion matrix" (Boyd, 2014) /
 "Colleague matrix" (Good, 1961) *)
colleagueMatrix[cc_] := With[{n = Length[cc] - 1},
   SparseArray[{{i_, j_} /; i == j + 1 :> 1/2,
      {i_, j_} /; i + 1 == j :> 1/(2 - Boole[i == 1])}, {n, n}] - 
    SparseArray[{{n, i_} :> cc[[i]]/(2 cc[[n + 1]])}, {n, n}]
   ];
(* Find the real roots of a truncated Chebyshev series
 representing a function over an interval [a,b] )
Options[chebRoots] = {( TBD )};
chebRoots::usage = 
  "chebRoots[c,{a,b}], c = {c0, c1,..., cn} Chebyshev coefficients, over the interval {a,b}
  computes the (real) roots in the interval {a,b}";
chebRoots[coeff_, dom_: {-1, 1}, OptionsPattern[]] := Module[{eigs},
  eigs = Eigenvalues@colleagueMatrix[coeff];
  roots = Sort@Rescale[
     Re@Select[
       eigs,
       Abs[Im[#]] < 1^-15 &&          (*  Im error tolerance )
         -1.0001 < Re[#] < 1.0001 &],  ( Re error tolerance *)
     {-1, 1}, dom]
  ]

Answer 2

Clear["Global`*"]

f[x_] = Abs[Hypergeometric1F1[1/4 (3 - (2*x)/I), 3/2, I]];

sol[n_Integer?Positive] := sol[n] = Quiet@Select[(FindRoot[
             f[x] == 0, {x, #, 2000 (n - 1), 2000 n},
             WorkingPrecision -> 15] & /@ Range[2000 (n - 1), 2000 n, 5]) // 
         Values // Flatten, Abs[f[#]] < 10^-10 &] // Round[#, 0.001] & // 
    Sort // DeleteDuplicates

The next expression is quite slow to evaluate

len = Length /@ (sol /@ Range[10])
(* {20, 8, 6, 6, 5, 4, 4, 3, 4, 3} *)

The cumulative number of roots is

Accumulate[len]
(* {20, 28, 34, 40, 45, 49, 53, 56, 60, 63} *)
plt[n_Integer?Positive] := plt[n] =
  Plot[f[x], {x, 2000 (n - 1), 2000 n},
   PlotPoints -> 200,
   MaxRecursion -> 10,
   WorkingPrecision -> 15,
   ImageSize -> Large,
   Epilog -> {Red, AbsolutePointSize[4],
     Point[{#, 0} & /@ sol[n]]}]
plt[1]

plt[10]

The roots get progressively further apart as x increases. Even out to x = 20,000 there are only 63 total roots.

Answer 3

Since from the plot, the roots are apparently almost periodic with slowly growing period, we can use the gap between a roots and the previous to guess the location of the next. This is essentially a refinement of the OP's approach, refining it by a more judicious choice of starting points.

PrintTemporary@Dynamic@{Clock@Infinity, foo};
rts = Re@DeleteDuplicates@Flatten@Values@NestList[
        {Last@#, 
          foo = 
           FindRoot[
            Hypergeometric1F1[1/4 (3 - (2*x)/I), 15/10, 
             I], {x, (x /. #) . {-1, 2} // Re}, 
            WorkingPrecision -> 32]} &,
        NSolve[
         Hypergeometric1F1[1/4 (3 - (2*x)/I), 15/10, I] == 0 && 
          2 < Re@x < 20 && -1/4096 < Im@x < 1/4096, {x}],
        100
        ]; // AbsoluteTiming
(*  {30.4636, Null}  *)
N@rts

In hindsight (you need only, say, 20 roots to get this hindsight), you could improve the guess slightly by using

(x /. #) . {-1, 2} + 9.869605623855932` // Re

for the initial guess for x in FindRoot. It saves about 40% on the execution time for 100 roots, and it's certainly worth doing if you want more roots than that. This hindsight comes from

Differences[N@rts[[;; 20]], 2]
(*  {..., 9.869605623855932`} *)

You can save a little more time (2-3%) using Last@Differences[N@rts, 2], but you have to spend 30 seconds to compute 100 roots; whereas, computing the first 20 roots takes only 0.35 sec. FWIW, in case you can use it and since I've computed it, the 100th 2nd-difference is

9.869604402607365` 

Answer 4

Your function is very similar, and asymptotically equal, to $g(x)=\frac{e^{i/2} \sin \sqrt{2x}}{\sqrt{2x}}$:

f[x_] = Hypergeometric1F1[(3 + 2 I x)/4, 3/2, I];
g[x_] = E^(I/2) Sinc[Sqrt[2 x]];
ReImPlot[{f[x], g[x]}, {x, 0, 300}]

This means that the zeros of $|f(x)|$ are close to the zeros of $|g(x)|$, which are at $\sqrt{2x_n}=n\pi$, or $x_n=\frac12n^2\pi^2$. Use these as starting points for FindRoot:

Clear[z];
z[n_Integer?Positive] := 
  z[n] = x /. FindRoot[Abs[f[x]] == 0, {x, n^2*π^2/2}]
z[1]
(*    4.79291    *)
z[2]
(*    19.579    *)
z[1000]
(*    4.934810^6    )

Actually, $e^{-i/2} f(x)$ is a real-valued function, so we can look for its roots more easily (because it has zero crossings, instead of the infinitely sharp kinks of $|f(x)|$:

Clear[z];
z[n_Integer?Positive] := 
  z[n] = x /. FindRoot[Re[E^(-I/2) f[x]] == 0, {x, n^2*π^2/2}]

Faster and no warnings:

z[1]
(*    4.79291    *)
z[2]
(*    19.579    *)
z[1000]
(*    4.934810^6    )