Two substitutions fail, so do I forget some earlier steps?
For
Cos[x] == Sin[(1/2)*Pi + x] /. x -> (1/2)*x = true
I don't get the final answer, but only true.
Cos[(1/2)*x] == Sin[(1/2)*Pi + (1/2)*x] (final answer)
A second derivation case :
Sin[x] == 2*Cos[x/2]*Sin[x/2] /. Cos[(1/2)*x] -> Sin[(1/2)*Pi + (1/2)*x] (*no substition possible *)
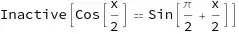
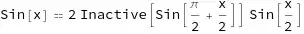
Trace[Cos[x] == Sin[(1/2)*Pi + x] /. x -> (1/2)*x]. Note that the initial equation evaluates toTruebefore the replacement ever comes into play. – Bob Hanlon Apr 10 '22 at 20:45Trace; highlight it in Mathematica and pressF1for help. – Bob Hanlon Apr 14 '22 at 17:48