6

The following is a condensed version of a lengthy expression. My objective is to eliminate nonlinear terms from an expression.

The vector containing the variables is:

veclst = {Subscript[A, 11], Subscript[A, 13], Subscript[A, 15]};

The reduced form of the expression is:

expr = a Subscript[A, 11] Subscript[A, 13] + b Subscript[A, 15] + 
c Subscript[A, 15] Subscript[A, 13] + d Subscript[A, 13]^2

My objective is to eliminate nonlinear terms in the expression (expression) in terms of the variables specified in veclst.

I appreciate your assistance in advance.

qahtah
  • 1,397
  • 6
  • 14

3 Answers3

6

Try This:

Total[Map[If[Total[Exponent[#, veclst]] > 1, Nothing, #] &, MonomialList[expr]]]

(b Subscript[A, 15])
E. Chan-López
  • 23,117
  • 3
  • 21
  • 44
6

Since

 Internal`LinearQ[5,x]

Gives false, (is this a bug or by design?) as per comment below, the following version accounts for such cases.

veclst = {Subscript[A, 11], Subscript[A, 13], Subscript[A, 15]};
expr = a Subscript[A, 11] Subscript[A, 13] + b Subscript[A, 15] + 
  c Subscript[A, 15] Subscript[A, 13] + d Subscript[A, 13]^2 + 5 + x;
List @@ expr

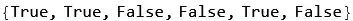
Mathematica graphics

And now do (*thanks to hints below for shorter code *)

sel = If[DisjointQ[Variables[#],veclst],True,Internal`LinearQ[#,veclst]] & /@List@@expr

Mathematica graphics

Then

Pick[expr, sel] (*shorter version thanks to Michael E2 *)

Mathematica graphics

Old answer

Another option is to use Internal`LinearQ

You can find the non-linear term using

sel = Internal`LinearQ[#, veclst] & /@ List @@ expr

Mathematica graphics

So only the 3rd term is linear. Now you can do

Total@Pick[List @@ expr, sel]

Mathematica graphics

Nasser
  • 143,286
  • 11
  • 154
  • 359
6

Another way:

CoefficientArrays[expr, veclst][[2]] . veclst

The polynomial does not need to be multiplied out:

SeedRandom[0];
var = {x, y, z};
poly = (1 + var . RandomInteger[2, 3])^2 *
    (1 - var . RandomInteger[2, 3])^3;
CoefficientArrays[poly, var][[2]] . var

(*  4 x + 4 y - 4 z  *)

Yet another way:

SeriesCoefficient[poly /. Thread[var -> t*var], {t, 0, 1}]

(*  4 (x + y - z)  *)

To get the degree-1 terms and lower:

Either of these (the first is how the docs show to do it for higher degree, but deg ≤ 1 can be done with Apply):

Fold[#1 + #2 . veclst &, CoefficientArrays[expr, veclst][[;; 2]]]
(* OR *)
#1 + #2 . veclst & @@ CoefficientArrays[poly, veclst][[;; 2]]

And

SeedRandom[0];
var = {x, y, z};
poly = (1 + var . RandomInteger[2, 3])^2*(1 - 
      var . RandomInteger[2, 3])^3;
Fold[#1 + #2 . var &, CoefficientArrays[poly, var][[;; 2]]]
(* OR *)
#1 + #2 . var & @@ CoefficientArrays[poly, var][[;; 2]]

(*  1 + 4 x + 4 y - 4 z  *)

Yet another way:

Normal@Series[poly /. Thread[var -> t*var], {t, 0, 1}] /. t -> 1

(*  1 + 4 (x + y - z)  *)
Michael E2
  • 235,386
  • 17
  • 334
  • 747
  • Thanks @Michael for your solution. Your code exculdes constant terms that don't have any variable. – qahtah Apr 12 '22 at 22:05
  • @qahtah Constant terms are not linear, at least in some contexts, and there are none in your example (or the other answers). If you want them, they can be included very easily: add CoefficientArrays[poly, var][[1]] to the rest. Let me know if you want it, and I'll add it to the code. – Michael E2 Apr 12 '22 at 22:24
  • Thanks @Michael Acutally what i needed was to remove higher order terms and keep lower order ones including the cosntant terms. – qahtah Apr 12 '22 at 22:49
  • @qahtah OK, I added the codes for each method. – Michael E2 Apr 12 '22 at 22:56