How to get all nodes in Tree?

Question

What is the most efficient way to get the nodes of a Tree?

tree = Tree[1, {Tree[    2, {Tree[5, {Tree[12, None], Tree[13, None]}], Tree[6, None]}],    Tree[3, {Tree[7, {Tree[14, None], Tree[15, None], Tree[16, None]}],      Tree[8, None], Tree[9, None]}],    Tree[4, {Tree[10, {Tree[17, None], Tree[18, None], Tree[19, None]}],      Tree[11, None]}]}];
Sort@Reap[TreeScan[Sow, tree]][[2, 1]] (* this seems wrong *)

Desired output: Range[19]

Follow-up: is there a way to get Annotate to work on Tree to store data in each node?

Could you please mention the desired output for your example? — Syed, Apr 16 '22 at 05:03
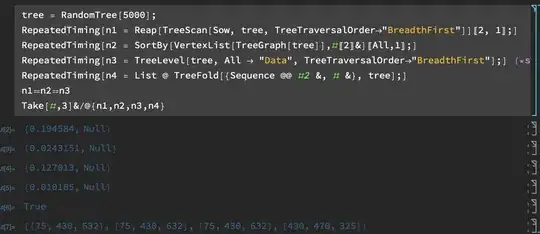
Are you aware that node 4 appears twice? Maybe you meant to use Tree[1, {Tree[ 2, {Tree[5, {Tree[12, None], Tree[13, None]}], Tree[6, None]}], Tree[3, {Tree[7, {Tree[14, None], Tree[15, None], Tree[16, None]}], Tree[8, None], Tree[9, None]}], Tree[4, {Tree[10, {Tree[17, None], Tree[18, None], Tree[19, None]}], Tree[11, None]}]}], — Henrik Schumacher, Apr 16 '22 at 16:58
I don't know anything about the Tree data structure or if it's documented to work with VertexList, but it seems to. ContainsExactly[VertexList[tree][[All, 1]], Range[19]] returns True. — Jason B., Apr 18 '22 at 19:03
@M.R after you edited your question, the following: Sort@Reap[TreeScan[Sow, tree]][[2, 1]] == Range@19 yields True. Can I ask for two things: one can you verify that, i.e that I did not make any mistakes? Two, do you still want a solution different than Sort@Reap[TreeScan[Sow, tree]][[2, 1]]? Could you explain why? Many thanks! — bmf, Apr 21 '22 at 20:11

user5601 · Accepted Answer · 2022-05-16T20:06:56.747

Looks like TreeGraph+VertexList+SortBy is the most efficient for Breadth First Search:

tree = RandomTree[5000];
RepeatedTiming[n1 = Reap[TreeScan[Sow, tree, TreeTraversalOrder->"BreadthFirst"]][[2, 1]];]
RepeatedTiming[n2 = SortBy[VertexList[TreeGraph[tree]],#[[2]]&][[All,1]];]
RepeatedTiming[n3 = TreeLevel[tree, All -> "Data", TreeTraversalOrder->"BreadthFirst"];] 
RepeatedTiming[n4 = List @ TreeFold[{Sequence @@ #2 &, # &}, tree];] (* wrong *)
n1==n2==n3
Take[#,3]&/@{n1,n2,n3,n4}

score 3 · Answer 2 · answered May 10 '22 at 13:08

3

The documented way using only Trees functionality is:

TreeLevel[tree, All -> "Data"]

answered May 10 '22 at 13:08

Ian Ford

521
5
3

1

This is the simplest, but doesn't seem to be the fastest. Also is the root missing? Length@TreeLevel[RandomTree[2], All -> "Data"] is 1 but should be 2. – user5601 May 12 '22 at 21:51
@user5601 Length @ TreeLevel[RandomTree[2], All -> "Data"] gives 2 for me in 13.0.1, what version are you using? – Ian Ford May 13 '22 at 22:55
1

A faster approach is List @ TreeFold[{Sequence @@ #2 &, # &}, tree]. TreeLevel itself could be sped up. – Ian Ford May 13 '22 at 22:58
1

Thanks that does seem faster, but can you do BreadthFirst? – user5601 May 16 '22 at 17:52
1

That TreeFold doesn't work at all for me... tree=Tree[1, {Tree[2, None], Tree[3, {Tree[4, None], Tree[5, None], Tree[6, None]}], Tree[7, None]}];List @ TreeFold[{Sequence @@ #2 &, #&}, tree] (*{2,4,5,6,7}*) – M.R. May 16 '22 at 19:44
@user5601 There's not a straight forward way to get the data in a breadth-first order with TreeFold since it collects the data of parents and children in a bottom-up, depth-first order. – Ian Ford May 17 '22 at 18:44
1

@M.R. Sorry, my previous comment incorrectly gives just the data of the leaves. lericr's answer Flatten@TreeFold[List,tree] gives the data of all nodes. – Ian Ford May 17 '22 at 18:51
@IanFord That command is still does not work as BFS – M.R. May 17 '22 at 18:56

score 1 · Answer 3 · edited Apr 18 '22 at 18:29

1

TreeLeaves[tree]

Or maybe

TreeCases[tree, _]

Or maybe

Flatten @ TreeFold[List, tree]

You might want to peruse http://reference.wolfram.com/language/guide/ComputationOnTrees.html

edited Apr 18 '22 at 18:29

M.R.

31,425
8
90
281

answered Apr 15 '22 at 23:31

lericr

27,668
1
18
64

Three points: TreeLeaves doesn't return the root nor does it strip the nodes out; TreeCases returns subtrees - not what I want; and TreeFold maintains the structure which is inefficient for large trees. – M.R. Apr 16 '22 at 01:21

score -1 · Answer 4 · edited Apr 18 '22 at 22:37

-1

You could try to traverse the tree and return every leaf, collecting them using Reap. E.g.:

Reap[
  TreeScan[Sow, tree]
][[2,1]]
(* {11, 12, 4, 5, 2, 13, 14, 15, 6, 7, 8, 3, 16, 17, 18, 9, 10, 4, 1} *)

edited Apr 18 '22 at 22:37

Jason B.

68,381
3
139
286

answered Apr 16 '22 at 15:20

Daniel Huber

51,463
1
23
57

1

that's was my starting point see above – M.R. Apr 18 '22 at 16:22
@M.R. - then you had the answer all along! – Jason B. May 10 '22 at 20:34

How to get all nodes in Tree?

4 Answers4