According to the error message:
NDSolve::nlnum1: "The function value {0} is not a list of numbers with dimensions {25} when the arguments are {50.,{<<25>>}."
I think you should feed a 25-length list of 0 to n[x,t] in the WhenEvent:
WhenEvent[t > 50, n[x, t] -> ConstantArray[0, 25]]
Plot the result:
Plot3D[Evaluate[n[x, t] /. sol], {x, 0, l}, {t, 0, 100}, PlotPoints -> 50]
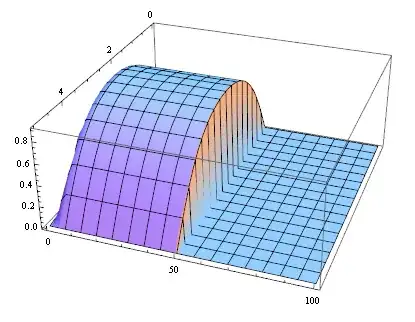
Edit:
According to the documentation, NDSolve automatically does processing for discontinuous functions like Sign, so here an alternative way which do not require manual specifying the number of grid nodes (i.e. 25):
sol2 = NDSolve[{
Derivative[0, 1][n][x, t] ==
d2*Derivative[2, 0][n][x, t] +
r*Sign[50 - t]*n[x, t]*(1 - Sign[50 - t]*n[x, t]),
n[x, 0] == 0.1*x*(1 - x/l),
n[0, t] == 0,
n[l, t] == 0},
{n}, {x, 0, l}, {t, 0, 100}]
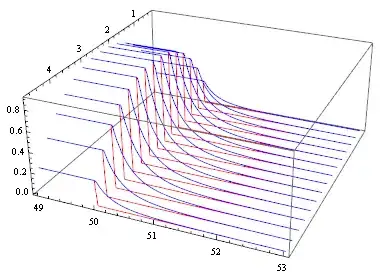
Note the difference near the discontinuity line between this solution and sol by above WhenEvent:
Show[
MapThread[Plot3D[
Evaluate[n[x, t] /. #1], {x, 0, l}, {t, 49, 53},
PlotPoints -> 50, PlotStyle -> None,
MeshFunctions -> (#1 &), MeshStyle -> #2,
BoundaryStyle -> None, PlotRange -> All
] &,
{{sol, sol2}, {Red, Blue}}
]]
Edit 2:
Using WhenEvent with automatic detecting the x-grid:
<< DifferentialEquations`InterpolatingFunctionAnatomy`
Clear[xGridExtractor]
xGridExtractor[f_] := InterpolatingFunctionCoordinates[Head[f]][[1]]
sol = NDSolve[
{
Derivative[0, 1][n][x, t] == d2*Derivative[2, 0][n][x, t] + r*n[x, t]*(1-n[x, t]),
n[x, 0] == 0.1*x*(1 - x/l),
n[0, t] == 0,
n[l, t] == 0,
WhenEvent[t > 50, n[x, t] -> 0*xGridExtractor[n[x, t]]]
},
{n}, {x, 0, l}, {t, 0, 100}]
Edit 3:
According to OP's comment, here is how to reset the initial condition along $t=50$ in a more general sense:
sol = NDSolve[
{
Derivative[0, 1][n][x, t] == d2*Derivative[2, 0][n][x, t] + r*n[x, t]*(1-n[x, t]),
n[x, 0] == 0.1*x*(1 - x/l),
n[0, t] == 0,
n[l, t] == 0,
WhenEvent[t > 50, n[x, t] -> (.5 Head[n[x, t]] /@ xGridExtractor[n[x, t]])]
},
{n}, {x, 0, l}, {t, 0, 100}]
Plot3D[Evaluate[n[x, t] /. sol], {x, 0, l}, {t, 49, 51},
PlotPoints -> 50, MeshFunctions -> {#2 &, #3 &}, Exclusions -> t == 50]




l,d2, etc.), it's hard to test. Could you add those to the question? – Michael E2 Jun 09 '13 at 05:08