I am trying to numerically solve some nonlinear partial differential equations similar to the example given below, for which I have been unable to obtain stable numerical solutions due to some peculiar features of the equations. There is a case for which a series solution exists for the steady-state solution, but I am unsure how to impose suitable boundary conditions so that the numerical solution of the full time-dependent equation is more stable and will converge to the desired steady-state solution.
Background:
An example which displays the sorts of features I have been dealing with is the following equation, which shows up in a few papers, such as this paper that I will focus on for the purposes of this post. I have modified the equation in the paper to eliminate some constants and make the time-like variable positive, and shifting their $u$ by a divergent but unimportant function of $t$ so that $\lim_{t \rightarrow +\infty} u(t,x,y) \equiv u_\ast(x,y) = 0$ is actually a valid steady-state solution, as claimed by [1]. (See the note at the end of the post for the explicit modifications I made) The resulting equation for $u(t,x,y)$ is
$$u_t(t,x,y) = (d+2) u - d~y~u_y - \frac{1 + u_{xy}}{\sqrt{(1+u_{xy})^2 - u_{xx} u_{yy}}} + 1,$$
with initial condition $u(0,x,y) \equiv u_0(x,y)$, where $u_t = \frac{\partial u}{\partial t}$, etc., and $d > 0$ is a parameter. The domains are $t \in [0,\infty)$, $y \in [0, \infty)$, and $x \in \mathbb{R}$. I should stress that although this looks a bit like a nonlinear diffusion equation, the quantity $u(t,x,y)$ is not a physical quantity like a concentration, but is a more abstract object. Notably, the IC we will look at below is unbounded as $|x|$ or $y \rightarrow \infty$.
Of particular interest are the possible fixed point solutions $u_\ast(x,y)$, and perturbations away from these solutions. Being a nonlinear equation there are many possible fixed point solutions; these are usually restricted to certain families based on symmetries of the model, or other properties of the initial condition that are preserved by the dynamics, and the fact that the fixed point solution must exist for all $y$ and $x$ on the domain. We are interested in solutions that are polynomially bounded in $y$. In particular, we expect $u_\ast(x,y) \sim y^{1+2/d}$ for large $y$. I am not sure anyone knows what the appropriate asymptotic behaviors are as $|x| \rightarrow \infty$.
The initial condition we'll focus on here is $$u_0(x,y) = g^0_{12}~x y^2/2 + g^0_{22}~x^2 y^2/4,$$ with parameters $g^0_{12},~g^0_{22} > 0.$ The authors of [1] argue that a series expansion of the solution $u(t,x,y)$ around $x = 0, y = 0$ will not contain any binomial terms $x^m y^n$ for which $m > n$. One can check that $u_\ast(x,y) = 0$ is a fixed point solution that is stable to any perturbation that obeys this restriction when $d > 2$.
When $d < 2$, the authors show the trivial solution becomes linearly unstable to a non-trivial solution, which they determine via a power series by showing that the coefficients $g_{mn} \equiv \frac{\partial^{m+n}u^\ast}{\partial x^m \partial y^n}\Big|_{x=y=0}$ obey a chain of dependencies that allows them to be evaluated iteratively: the equation for $g_{22}$ is closed, and determines $g_{12}$, which determines $g_{33}$, and so on. The pattern is $g_{n,n} \rightarrow g_{n-1,n} \rightarrow \dots \rightarrow g_{1,n} \rightarrow g_{n+1,n+1} \rightarrow \dots$, starting with $n = 2$. (See Fig. 2 of [1], and a minimal Mathematica code to compute these solutions below).
My issue: I would like to solve the PDE numerically and see the decay to $0$ for $d > 2$ and convergence to the solution that matches the series near $(x,y) = (0,0)$ for $d < 2$. A straightforward attempt at a solution does not yield good results: we use a finite range of $x$ and $y$, without explicitly imposing boundary conditions, and the solutions initially appear to be heading in the expected directions, but quickly become numerically unstable at finite $t$. Here is a minimal working example that attempts to solve the PDE:
(* PDE for u[t,x,y] with parameters d, g12, g22 *)
ucoag[d_, g12_, g22_] :=
NDSolve[{D[u[t, x, y], t] == (d + 2)*u[t, x, y] -
d*y*D[u[t, x, y], y] - (1 + D[u[t, x, y], x, y])/
Sqrt[(1 + D[u[t, x, y], x, y])^2 -
D[u[t, x, y], x, x]*D[u[t, x, y], y, y]] + 1,
u[0, x, y] == g12*x*y^2/2 + g22*x^2*y^2/4},
u, {t, 0, 30}, {x, -1.0, 1.0}, {y, 0, 10}]
(* Case 1: d = 2.1 > 0. Solution expected to decay to 0. *)
ud2p1 = ucoag[2.1, 0.01, 0.01]
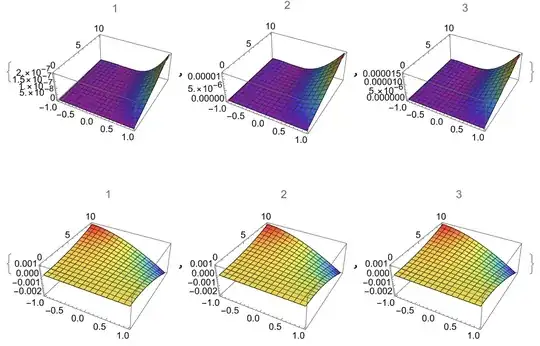
(* Plot result. Numerical solution shows signs of instability around t ~ 22. *)
Manipulate[
Plot3D[{Evaluate[u[t, x, y] /. ud2p1]}, {x, -1, 1}, {y, 0, 10}], {t,
0, 30}]
(* Case 2: d = 1.9 < 2. Expect convergence to non-trivial solution that matches series expansion near (x,y) = (0,0) *)
ud1p9 = ucoag[1.9, 0.01, 0.01]
(* Plot result. Numerical solution shows signs of instability around t ~ 13. *)
Manipulate[
Plot3D[{Evaluate[u[t, x, y] /. ud1p9]}, {x, -1, 1}, {y, 0, 10}], {t,
0, 30}]
(* Plot first derivative wrt x at x=0 and compare to analytical series at d = 1.9. *)
Manipulate[
Plot[{Evaluate[D[u[t, x, y], x] /. {x -> 0} /. ud1p9],
0.050000000000000044y^2 + 0.00041666666666666767 y^3 -
0.000018857258812615815y^4 + 7.675839376828031^-7 y^5 -
1.506757897829043`^-8 y^6}, {y, 0, 0.5}], {t, 0, 12}]
Mathematica throws a warning because of the lack of boundary conditions, but otherwise will provide a solution for all $t$ specified (though the result is meaningless beyond a finite $t$ because the numerical instability will eventually cause the solution to become complex). My understanding is that Mathematica computes derivatives using only internal points when BCs are not supplied (see here and here), depending on Method. This would be similar to what has been done in solving simpler versions of similar equations numerically, using 5-point stencils.
I would assume that providing boundary conditions would help stabilize the numerical solution, but it is unclear what boundary conditions ought to be imposed. Due to the unboundedness of the solutions at one or more edges of the infinite domain, I am not sure what would be a good choice. A large constant seems too naive (and result in inconsistent boundary warnings). Perhaps implementing a polynomial bound in $y$ would help, but I am not sure how to do so.
I would appreciate any help making Mathematica's evaluation of this PDE more stable! Thank you.
Other notes:
[1]'s Eq. 13 reads $$u_\tau(\tau,\tilde{\chi},\chi) = -(d+2) u + d~\chi~u_\chi + \frac{\tilde{V}_d(1 + u_{\tilde{\chi}\chi})}{\sqrt{(1+u_{\tilde{\chi}\chi})^2 - u_{\tilde{\chi}\tilde{\chi}} u_{\chi\chi}}},$$ where the time-like parameter $\tau$ is negative and $\tilde{V}_d$ is a constant that depends on the parameter $d$. As written, $u(-\infty,\tilde{\chi},\chi) = 0$ is not a fixed point of this flow equation, because the authors ignore a constant offset, which does not play a role in their series solution but would diverge numerically. I explicitly removed this offset so that it does not contribute a diverging offset to the numerical solution, as well as change variables to make time positive, and to scale away the unimportant constant $\tilde{V}_d$. To be specific, to convert [1]'s Eq. 13 into the form given above and in the Mathematica code, I made the change of variables $u(\tau,\tilde{\chi},\chi) \rightarrow \tilde{V}_d u(-\tau,\tilde{\chi},\chi/\tilde{V}_d) + c(t)$, and set $t = -\tau$, $x = \tilde{\chi}$ and $y = \chi/\tilde{V}_d $. The offset can be removed by evaluating the right-hand-side at $(x,y) = (0,0)$ (for which $u(t,x=0,y=0)$ vanishes), which gives a differential equation for $c(t)$, $c_t = (d+2)c - 1$. We can then plug this into the full equation for the remaining piece $u$ to obtain the form given in this post.
I have tried using
Method -> {"PDEDiscretization" -> {"MethodOfLines", "SpatialDiscretization" -> {"TensorProductGrid", "MinPoints" -> {40, 140}}}}. I stopped evaluation after about an hour because my laptop sounded like it was going to catch fire.I looked into finite element methods, but I believe this PDE cannot be put into the required standard form for the nonlinear FEM solver to work.
Most work solving similar equations does not actually try to solve the full PDE with $x$ dependence, instead making additional approximations or truncations to eliminate the $x$-dependence entirely. For example, similar papers define a hierarchy of equations for $v_m(t,y) \equiv \left.\frac{\partial^m}{\partial x^m}u(t,x,y) \right|_{x = 0}$, which they close via an approximation (often $v_M(t,y) = 0$ for some $M$). In this case the initial conditions become sufficient to find a solution, though there may exist artifacts due to the truncation. Hence, it would be nice to directly solve the PDE for $u(t,x,y)$, if it's possible.
Here is some code for iteratively calculating the coefficients $g_{mn}$. It is a bit slow for nmax larger than 6 or so, and I suspect it could be vastly improved, but that is better left as the topic of a separate question. (Unfortunately AsymptoticDSolveValue does not work with PDEs yet).
(* Determine coefficients. g[2,2] == 2(2-d), g[1,2] == 2-d determined earlier. *)
nmax = 5; (* maximum degree of x and y desired in series approximation. Can take a while for larger values. *)
glist = DeleteCases[
Table[D[0 == ((d + 2)u[x, y] -
dyD[u[x, y], y] - (1 + D[u[x, y], x, y])/
Sqrt[(1 + D[u[x, y], x, y])^2 -
D[u[x, y], x, x]D[u[x, y], y, y]] + 1) /. {u ->
Function[{x, y},
Sum[g[k, l]x^ky^l/k!/l!, {l, 2, nmax}, {k, 1,
l}]]}, {x, m}, {y, n}] /. {x -> 0, y -> 0}, {n, 1,
nmax}, {m, 1, n}] /. {g[2, 2] -> -2 (-2 + d),
g[1, 2] -> -(-2 + d)} // Simplify // Flatten, True];
(* Solve for the remaining coefficients *)
gsoln = Solve[glist,
DeleteCases[
Table[g[m, n], {n, 2, nmax}, {m, 1, n}], {g[1, 2], g[2, 2]}] //
Flatten] // Flatten;
(* Plot the solution to the chosen order for, e.g., d = 1.9 )
Plot3D[{Sum[(g[k, l] /. {g[1, 2] -> 2 - d , g[2, 2] -> 2 (2 - d)} /.
gsoln /. {d -> 1.9})x^k*y^l/k!/l!, {l, 2, nmax}, {k, 1,
l}]}, {x, -1, 0}, {y, 0, 3}]

NDSolveyou use equation in the formD[u[t, x, y], t] == (d + 2)*u[t, x, y]-...while in the Latex form $u_t=(d-2)u-...$? Where is typo? – Alex Trounev Apr 26 '22 at 12:46Vd! Perhaps it's possible to solve the pde iteratively using FEM. – Ulrich Neumann Apr 27 '22 at 08:31c'[t]-(2+d) c[t](no offset1) . If the correct equation is confirmed I'll try to show you my iterative approach – Ulrich Neumann Apr 27 '22 at 17:02