How to find PlanarAngle[] across periodic boundaries?

Question

Suppose we have a collection of points selected as being within a certain radius (0.1) of myCenterPoint:

myCenterPoint = {0.48536, 0.496745};
myCenterNeighbors = {{0.48506, 0.518851}, {0.467608, 
  0.51639}, {0.456715, 0.489564}, {0.523108, 0.489627}, {0.448557, 
  0.485287}, {0.432191, 0.479128}, {0.545804, 0.506127}, {0.435738, 
  0.534355}, {0.438056, 0.538347}, {0.484009, 0.425348}, {0.549424, 
  0.462288}, {0.562333, 0.500577}, {0.409715, 0.51475}, {0.460376, 
  0.421197}, {0.540092, 0.438462}, {0.405604, 0.485177}, {0.560972, 
  0.534108}, {0.548135, 0.553546}, {0.457615, 0.581859}, {0.425488, 
  0.427731}, {0.478787, 0.404865}, {0.550746, 0.430695}, {0.404494, 
  0.44804}, {0.399277, 0.542863}};

All points lie within a $x$,$y$ range between $0$ and $1$, the domainRange. Now, I'd like to compute the PlanarAngle[] between the central point and every other neighbor. This is done by:

domainRange={0.0, 1.0};
centralAngles = 
  Table[PlanarAngle[myCentralPoint -> {{domainRange[[2]], myCenterNeighbors[[1]][[2]]},
  myCenterNeighbors[[i]]}], {i, 1, Length[myCenterNeighbors]}];

We can visualize that the angles indeed go through each point, by drawing arrows across them:

radiusArrow = 0.2;
Show[ListPlot[myCenterNeighbors, 
AspectRatio -> Automatic,
PlotRange -> {{0, 1}, {0, 1}}], 
Graphics[{Red, Arrow[AnglePath[myCenterPoint, {{radiusArrow, #}}] & /@ centralAngles]}]]

Getting:

Now, I have done the same for a point that is in the periphery of the spatial domain, using a distance function for periodic boundaries (meaning, the $radius<0.1$ neighborhood is calculated across the boundaries). My question is, how could I get the angles that take into consideration the periodicity of this domain? The solution should use the PlanarAngle[] function if possible.

Applying the same process as above is --of course-- a failure:

myPeripheryPoint = {0.00841536468074966`, 0.002197018919080307`};
myPeripheryNeighbors = {{0.03229560949868793`, 
    0.9865069071458752`}, {0.9795340627801099`, 
    0.0020868182730364726`}, {0.03858378647524385`, 
    0.012525407762965068`}, {0.9913160172244748`, 
    0.9570079562439078`}, {0.9917737197180683`, 
    0.04923062576084303`}, {0.05054580682579313`, 
    0.03983763666940843`}, {0.9848092367462769`, 
    0.9487060792639312`}, {0.9919193024256374`, 
    0.9443507696946527`}, {0.06593430284785717`, 
    0.9802315321816846`}, {0.03063567167293657`, 
    0.9399087243621003`}, {0.07729526444337176`, 
    0.011791675915653554`}, {0.9434979787548483`, 
    0.9682050073234711`}, {0.9829522482069939`, 
    0.9333879581233924`}, {0.937958402932543`, 
    0.023490997900727173`}, {0.036769273517222034`, 
    0.9335221301932126`}, {0.9893277043935138`, 
    0.9297962874690391`}, {0.980900667782586`, 
    0.9300759568484791`}, {0.930144399230207`, 
    0.017422280608305307`}, {0.03275323456438972`, 
    0.08278995189636573`}, {0.0905953216509523`, 
    0.02752181180818436`}, {0.0925328147605804`, 
    0.02146492818209489`}, {0.09764014967822088`, 
    0.9844617574268106`}, {0.9423197762714688`, 
    0.06654711398560131`}, {0.08407855645557638`, 
    0.0638776330353239`}, {0.04786712113942193`, 
    0.09224899111632401`}, {0.9251440827682063`, 
    0.9476726186386728`}, {0.05288034131659658`, 
    0.09169421967972102`}};
peripheryAngles = 
  Table[PlanarAngle[
    myPeripheryPoint -> {{domainRange[[2]], myPeripheryPoint[[2]]}, 
      myPeripheryNeighbors[[i]]}], {i, 1, 
    Length[myPeripheryNeighbors]}];
radiusArrow = 0.18;
Show[Graphics[{Red, 
   Arrow[AnglePath[myPeripheryPoint, {{radiusArrow, #}}] & /@ 
     peripheryAngles]},
  AspectRatio -> Automatic, PlotRange -> {{0.0, 1.0}, {0.0, 1.0}},
  Frame -> True, FrameStyle -> Directive[Black, 14]],
 ListPlot[myPeripheryNeighbors]]

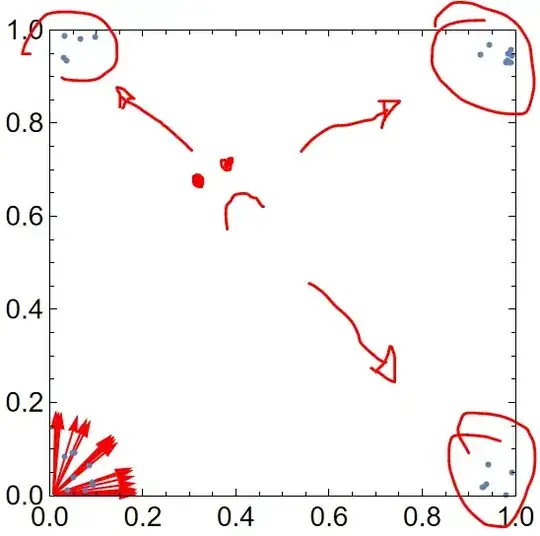
So, we'd end up with angles that go beyond the current domain, like these blue ones, corresponding to the direction of the points that lie out of the domain:

Thank you!

Edit1: If it's relevant --but I don't think so--, the way the distance from somePoint to allOtherPoints was calculated as follows:

(*To compute distance with periodic boundaries*)
myDistFunct[a_, b_, domainLength_] := 
  Norm@Mod[a - b, domainLength, -domainLength/2]
(The actual computation)
NearestTo[somePoint, {All, radiusDistance}, 
  DistanceFunction -> (myDistFunct[##, domainRange[[2]]] &)][
 allOtherPoints -> {"Index", "Element", "Distance"}]

Which was adapted from this answer.

I can't say that I understand the question. How does the first example you present with the center at roughly (0.5,0.5) relate to the other clusters at the Rectangle[ ] corners? Is the final region of interest limited by this? — Syed, Apr 28 '22 at 11:43
@Syed So, in the first example, there's a point at around (0.5,0.5) with a bunch other points nearby. The central, reference point, has some angles to the other points, as shown by the red arrows. In the second example, the reference point happens to be at one of the corners (left, bottom), and the neighbor points are within the neighborhood radius in a periodic boundary, but their directions are not "seen" correctly when the angles are calculated (red arrows should radiate around the point, instead of just pointing to the points on the 4 corners of the domain). Hope that helps, thanks! — TumbiSapichu, Apr 28 '22 at 16:58
You can find PlanarAngle for only those points that are within your region of interest. PlanarAngle doesn't know about your region. You can use RegionMember function before calculating planar angles. Or perhaps you want to filter the angles: e.g., at the lower left corner near (0,0) you can only allow angles between 0 and 90 degrees, perhaps and so on. I don't know of a mechanism for doing it using built-in functions. — Syed, Apr 28 '22 at 18:19

score 1 · Answer 1 · answered Apr 28 '22 at 20:19

Here's a function to move a point as close to the origin as possible. It turns out this can be done independently for each coordinate:

Remove[moveNearOrigin]
moveNearOrigin[point:{_?NumericQ...},r_?NumericQ]:=Mod[#+r/2,r]-r/2&/@point

The proof that the equation $\mathrm{mod}(x+r/2,r)-r/2$ is closest to 0 is actually quite slick: from the definition of $\mathrm{mod}$, $0\leq x+r/2<r$, thus our quantity has $-r/2\leq x<r/2$. I digress.

We'll map over the points using this function

peripheryAngles=PlanarAngle[
    myPeripheryPoint->{myPeripheryPoint+{0.,1.},moveNearOrigin[#,1]}
  ]&/@myPeripheryNeighbors

Now this assumes that the chosen origin is near $(0,0)$. Here's a version to handle that

peripheryAngles=PlanarAngle[
    moveNearOrigin[myPeripheryPoint,1]->
      {moveNearOrigin[myPeripheryPoint,1]+{0.,1.},moveNearOrigin[#,1]}
  ]&/@myPeripheryNeighbors

You can run the code with a myPeripheryPoint that is closer to a different corner to test this.

How to find PlanarAngle[] across periodic boundaries?

1 Answers1