The jumping problem when rolling a Reuleaux triangle

Question

I'm making an animation of a Reuleaux triangle rolling on a straight line like this

The animation generated by my code is not continuous. Is there a simple way to eliminate jumping?

Manipulate[
 Module[{reuleaux, s},
  reuleaux[t_] = {-Cos[Pi/3 (1 + 2 Floor[3 t])] +  Sqrt[3] Cos[Pi/6 + Pi t + Pi/3  Floor[3 t]],
  -Sin[Pi/3 (1 + 2 Floor[3 t])] + Sqrt[3] Sin[Pi/6 + Pi t + Pi/3  Floor[3 t]]};
  s[t_?NumericQ] := NIntegrate[Norm[reuleaux'[s]], {s, 0, t}];
  ParametricPlot[{s[u], 0} + (reuleaux[t] - reuleaux[u]).RotationMatrix[ArcTan @@ (reuleaux'[u])] // Evaluate,
  {t, 0, 1}, PlotRange -> {{-1, 7}, {-1, 2}}]
  ], {u, 0.001, 1 + 0.001}]

Reference link:
On rolling polygons and Reuleaux polygons
formula-to-create-a-reuleaux-polygon
How to roll a graph on the y-axis
How to plot a bicycle with square wheels

The problem stems from the fact that the rotation angle ArcTan @@ (reuleaux'[t]) is not a continuous function of t, which in turn stems from the fact that your parametrization of the curve has a discontinuous derivative at the corners. So when you get to one of the corners, the animation skips from rolling along one curve to rolling along the next curve, without pivoting around the corner in between these motions. Not immediately sure how to fix this, but I'll think on it further. — Michael Seifert, May 02 '22 at 16:36

Adam · Answer 1 · 2022-05-04T06:33:59.460

Daniel Huber's code seems to let the points and edges slide a little. In order to ensure no slippage, you need to use the perimeter of the shape: each arc has length $\pi/3$, so the distance between successive vertex rotations should be $\pi/3$.

This code is crude but gets the job done

With[{prims=Circle@@@({CirclePoints@3/√3,{1,1,1},{{2,3},{4,5},{0,1}}π/3}\[Transpose])},
Animate[Graphics@With[{mθ=Mod[θ,2π/3]},With[{tr={⌊3θ/(2π)⌋π/3,0}+
If[mθ<π/3,{mθ(π-√3)/π,1-Cos[π/6-mθ]/√3},{(2π-√3)/6-Cos[mθ]/√3,Sin[mθ]/√3}]},
{Point@tr,TranslationTransform[tr]@*RotationTransform[π/6-θ]/@prims,
Line/@{{{-1,1},{5,1}},{{-1,0},{5,0}}},Point@{π#/3-1/(2√3),0}&/@Range[0,4]}]],
{θ,0,7π/3},AnimationDirection->ForwardBackward]]

and you get something like

score 2 · Answer 2 · answered May 02 '22 at 21:10

With code from the Wolfram Demo project for a Reuleaux triangle from https://demonstrations.wolfram.com/ARotatingReuleauxTriangle/ and some small changes:

angle[vec_] := 
 Arg[First[vec] + I*Last[vec]] + If[Last[vec] >= 0, 0, 2*Pi]
centerpath[t_] := 
  Piecewise[{{{1 + Cos[Mod[t, 2 Pi/3] + 7 Pi/6] + 
       Sqrt[3]/3Sin[Mod[t, 2 Pi/3] + 7 Pi/6], 
      1 + Sin[Mod[t, 2 Pi/3] + 7 Pi/6] + 
       Sqrt[3]/3Cos[Mod[t, 2 Pi/3] + 7 Pi/6]}, 
     0 <= Mod[t, 2 Pi/3] < Pi/6},
    {{-1 - Sin[Mod[t, 2 Pi/3] + Pi] - 
       Sqrt[3]/3Cos[Mod[t, 2 Pi/3] + Pi], 
      1 + Cos[Mod[t, 2 Pi/3] + Pi] + 
       Sqrt[3]/3Sin[Mod[t, 2 Pi/3] + Pi]}, 
     Pi/6 <= Mod[t, 2 Pi/3] < Pi/3},
    {{-1 - Cos[Mod[t, 2 Pi/3] + 5 Pi/6] - 
       Sqrt[3]/3Sin[Mod[t, 2 Pi/3] + 5 Pi/6], -1 - 
       Sin[Mod[t, 2 Pi/3] + 5 Pi/6] - 
       Sqrt[3]/3Cos[Mod[t, 2 Pi/3] + 5 Pi/6]}, 
     Pi/3 <= Mod[t, 2 Pi/3] < Pi/2},
    {{ 1 + Sin[Mod[t, 2 Pi/3] + 2 Pi/3] + 
       Sqrt[3]/3Cos[Mod[t, 2 Pi/3] + 2 Pi/3], -1 - 
       Cos[Mod[t, 2 Pi/3] + 2 Pi/3] - 
       Sqrt[3]/3Sin[Mod[t, 2 Pi/3] + 2 Pi/3]}, 
     Pi/2 <= Mod[t, 2 Pi/3] < 2 Pi/3}}];
reuleaux[s_] := Module[{a, b, c},
  a = centerpath[s] + Sqrt[3]/32{Cos[-s], Sin[-s]};
  b = centerpath[s] + Sqrt[3]/32{Cos[-s + 2 Pi/3], Sin[-s + 2 Pi/3]};
  c = centerpath[s] + Sqrt[3]/32{Cos[-s + 4 Pi/3], Sin[-s + 4 Pi/3]};
  Graphics[{LightGray,
    Disk[a, 2, {angle[b - a], angle[b - a] + Pi/3}],
    Disk[b, 2, {angle[c - b], angle[c - b] + Pi/3}],
    Disk[c, 2, {angle[a - c], angle[a - c] + Pi/3}],
    Black,
    Circle[a, 2, {angle[b - a], angle[b - a] + Pi/3}],
    Circle[b, 2, {angle[c - b], angle[c - b] + Pi/3}],
    Circle[c, 2, {angle[a - c], angle[a - c] + Pi/3}],
    PointSize[.02], Black,
    Point[a],
    Point[b],
    Point[c],
    Point[(a + b + c)/3],
    Line[{{1, -1}, {1, 1}, {-1, 1}, {-1, -1}, {1, -1}}]},
   Axes -> True]
  ]

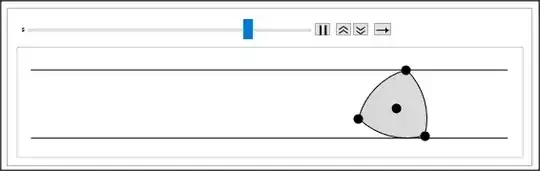
And the addition of the x- movement we can create the following animation:

Animate[Graphics[{Translate[reuleaux[s][[1]], {Sqrt[3] s, 0}],
   Line[{{{-2, -1}, {12, -1}}, {{-2, 1}, {12, 1}}}]} , 
  PlotRange -> {{-2, 12}, {-1.2, 1.2}}, ImageSize -> 500], {s, -0.1 , 
  2 Pi}]

The jumping problem when rolling a Reuleaux triangle

2 Answers2