PlotRangeClipping is not working correctly with ListLinePlot?

Question

Bug introduced in 12.3 or earlier and persisting through 13.1.0

data = Table[{x, Sin[3 x]}, {x, -4, 4, 0.1}];
plot=ListLinePlot[data, Frame -> True, PlotRange -> {{-1, 1}, {-0.5, 0.5}},
  ImageSize -> Automatic -> {150, 100}, PlotStyle -> Directive[Thickness[0.01], Red, CapForm["Butt"]], 
 PlotRangeClipping -> True];
Export["C:\plot.png", plot, 
 ImageResolution -> 800]

Update#1

As noted in the comment by @cvgmt the above bug is fixed in Mathematica 13.0.1, but adding ColorFunction -> Hue raises the problem again even in Mathematica 13.0.1:

I tried RegionFunction to solve this silly MMA problem, but it did not work with ListLinePlot as it does with Plot.

plot = ListLinePlot[data, Frame -> True, 
  PlotRange -> {{-1, 1}, {-0.5, 0.5}}, 
  ImageSize -> Automatic -> {150, 100}, ColorFunction -> Hue, 
  PlotStyle -> Directive[Thickness[0.01], Red, CapForm["Butt"]], 
  PlotRangeClipping -> True, RegionFunction -> (-1 <= # <= 1 &)]

You have discovered another buggy case for PlotRangeClipping which wasn't fixed in version 13.0.1. Please report it to the tech support. — Alexey Popkov, May 08 '22 at 17:48
any workaround for the moment? and why RegionFunction does not work with ListLinePlot? — MMA13, May 08 '22 at 19:03
Try Options[ListLinePlot, RegionFunction]. You will get the error message: "RegionFunction is not a known option for ListLinePlot." And see my answer below. — Alexey Popkov, May 09 '22 at 03:13
From the other side, on the Docs page for RegionFunction ListLinePlot is listed as supported function. Hence non-working RegionFunction is another bug of ListLinePlot. Please report it too. — Alexey Popkov, May 09 '22 at 03:22

Alexey Popkov · Accepted Answer · 2022-05-09T13:24:38.307

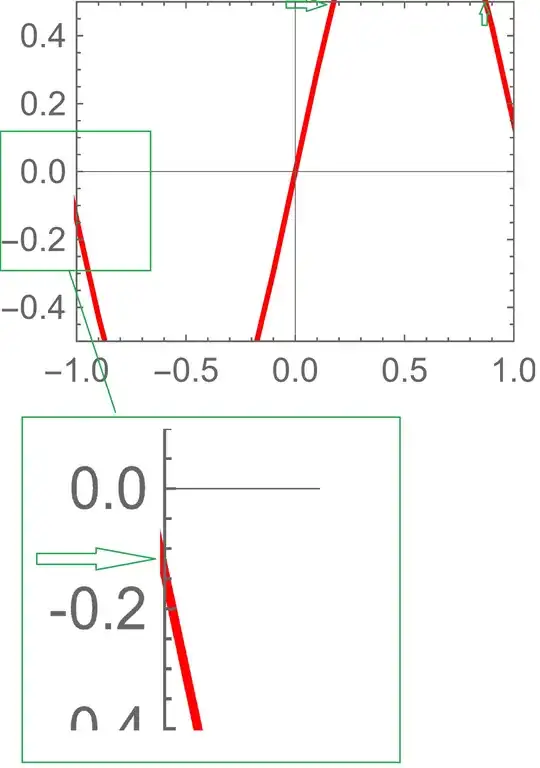
You have discovered another buggy case for PlotRangeClipping which wasn't fixed in version 13.0.1. It is worth to know that this bug isn't present in version 8.0.4, so it is a backslide bug. Please report this to the tech support.

As a workaround you can add above the plotted line a white Polygon with a hole. The hole should exactly cover the whole PlotRange:

data = Table[{x, Sin[3 x]}, {x, -4, 4, 0.1}];
plot = ListLinePlot[data, Frame -> True, FrameStyle -> Thickness[0.005], 
   PlotRange -> {{-1, 1}, {-0.5, 0.5}}, ImageSize -> Automatic -> {150, 100}, 
   PlotStyle -> Directive[Thickness[0.01], Red, CapForm["Butt"]], 
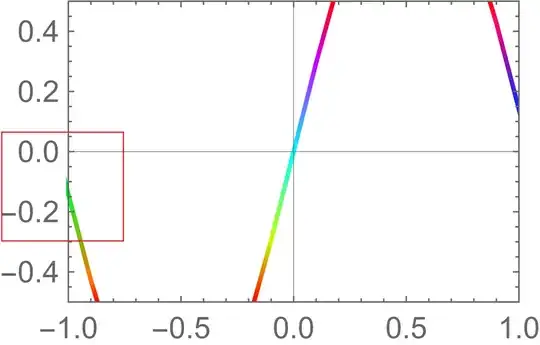
   PlotRangeClipping -> True, ColorFunction -> Hue];
plot2 = Show[plot,
   Graphics[{White, EdgeForm[None],
     Polygon[{{-1.1, -0.51}, {1.1, -0.51}, {1.1, 0.51}, {-1.1, 0.51}} ->
       {{-1, -0.5}, {1, -0.5}, {1, 0.5}, {-1, 0.5}}]}]];
Export["plot.png", plot2, ImageResolution -> 800]

The exported file (Mathematica 13.0.1):

You can automate the above approach with the function fixClipping defined below:

Clear[ClippingPolygon, fixClipping]
ClippingPolygon[{{xmin_, xmax_}, {ymin_, ymax_}}, padding_ : 0.05] := 
  Module[{hole, dX, dY, outer},
   hole = {{xmin, ymin}, {xmax, ymin}, {xmax, ymax}, {xmin, ymax}};
   dX = (xmax - xmin)*padding;
   dY = (ymax - ymin)*padding;
   outer = {{xmin - dX, ymin - dY}, {xmax + dX, ymin - dY}, 
            {xmax + dX, ymax + dY}, {xmin - dX, ymax + dY}};
   Polygon[outer -> hole]];
fixClipping[plot_Graphics] := Module[{pr, prp, FullPlotRange},
  {pr, prp} = Values@AbsoluteOptions[plot, {PlotRange, PlotRangePadding}];
  FullPlotRange = pr + prp*{{-1, 1}, {-1, 1}};
  Show[plot, Graphics[{White, EdgeForm[None], ClippingPolygon[FullPlotRange]}]]]

How it can be used:

plotFixed = fixClipping@plot;
Export["plot.png", plotFixed, ImageResolution -> 800]

(The result is as shown above.)

In the Mathematica versions 13.0 and above this function should work correctly with non-explicit PlotRange and PlotRangePadding specifications (for example, PlotRange -> {{-1, 1}, All}, PlotRangePadding -> Scaled[.05]). In the earlier versions for obtaining the padded plot range (FullPlotRange in fixClipping) one can use Carl Woll's GraphicsInformation instead of AbsoluteOptions.

UPDATE in responce to comments

Here is another solution which doesn't force rasterization and allows exporting the figure in vectors as PDF:

Clear[ClippingRectangles, fixClipping2]
ClippingRectangles[{{xmin_, xmax_}, {ymin_, ymax_}}, padding_ : 0.05, pixelFix_ : 0.01] :=
  Module[{pX, fX, pY, fY, pol1, pol2, pol3, pol4},
   {pX, fX} = (xmax - xmin)*{padding, pixelFix};
   {pY, fY} = (ymax - ymin)*{padding, pixelFix};
   pol1 = Rectangle[{xmin - pX, ymin - pY}, {xmin - fX, ymax + pY}];
   pol2 = Rectangle[{xmax + fX, ymin - pY}, {xmax + pX, ymax + pY}];
   pol3 = Rectangle[{xmin - pX, ymin - pY}, {xmax + pX, ymin - fY}];
   pol4 = Rectangle[{xmin - pX, ymax + fY}, {xmax + pX, ymax + pY}];
   GraphicsGroup[{pol1, pol2, pol3, pol4}]
   ];
fixClipping2[plot_Graphics] := 
 Module[{pr, prp, FullPlotRange}, {pr, prp} = 
   Values@AbsoluteOptions[plot, {PlotRange, PlotRangePadding}];
  FullPlotRange = pr + prp*{{-1, 1}, {-1, 1}};
  Show[plot, Graphics[{White, EdgeForm[None], ClippingRectangles[FullPlotRange]}]]]

How to use:

plotFixed = fixClipping2@plot;
Export["plot.pdf", plotFixed]

The disadvantage of this method is that in some situations it may be required to adjust the value of pixelFix manually. This value is required due to limited precision of relative positioning of the primitives on the plot by the FrontEnd. Sometimes they may be off by "1 pixel" despite the fact that FrontEnd exports the figure to a high-precision vector format.

thanks for the detailed answer. However, this solution is not allowed to export a vector-style plot as pdf or eps. — MMA13, May 09 '22 at 12:09
@valarmorghulis I updated the answer with an alternative implementation, which doesn't force rasterization when exporting to vector formats. — Alexey Popkov, May 09 '22 at 13:25
@valarmorghulis I've found that for your plots Mathematica 13.0.1 has no clipping problems when exporting them as PDF. So the workaround is necessary only for exporting to raster formats. — Alexey Popkov, May 09 '22 at 14:08

PlotRangeClipping is not working correctly with ListLinePlot?

1 Answers1

Linked