Random graphs in Poincare disk

Question

The question is inspired by that article ( see Wiki as a first reading on the topic). This is an actual topic of modern mathematical physics. Here is my (partly successful) attempt to implement such graphs in Mathematica.

Let a graph be located in Disk[{0,0},r] (of hyperbolic radius R = ArcCosh[1 + 2/(1 - r^2)]). First, we create a random set of its vertices by

r = 99/100; R = ArcCosh[1 + 2/(1 - r^2)]; SeedRandom[1234]; 
vertices = Table[{RandomVariate[UniformDistribution[{0, 2*Pi}], 1][[1]], 
RandomVariate[ProbabilityDistribution[Sinh[t]/(-1 + Cosh[R]), {t, 0, R}], 1][[1]]}, {j, 1, 30}];

, following formula (1) from the linked article with \[Alpha]=1. Second, we create a random set of its edges by

edges = Apply[UndirectedEdge, #] & /@ RandomSample[Subsets[vertices, {2}], 80];

We choose 80 random two-elemented subsets of vertices by RandomSample[Subsets[vertices, {2}], 80] and then transform the ones to edges by Apply[UndirectedEdge, #] & /@.

Now

Graph[vertices, edges, VertexCoordinates -> 
Table[vertices[[j]] -> {vertices[[j]][[2]]*Cos[vertices[[j]][[1]]], 
vertices[[j]][[2]]*Sin[vertices[[j]][[1]]]}, {j, 1,  Dimensions[vertices][[1]]}]]

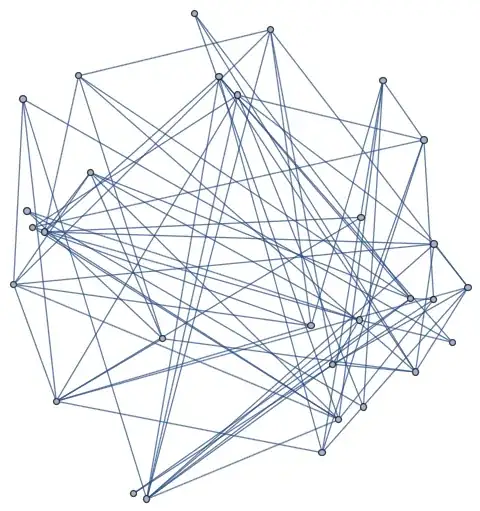The coordinates of vertices are polar $(\phi,r)$ so we have to change these to cartesian coordinates.

The above is a somewhat unfinished work.

(i) Physicists often use the following construction: any two vertices $u$ and $v$ are connected by an edge if their hyperbolic distance $\textrm{dist}H(u, v)$ is below a certain number $\rho$. Neither BernoulliGraphDistribution nor BarabasiAlbertGraphDistribution realize it. How to do it?

(ii) In the above edges are drawn as lines. How to draw edges as hyperbolic lines ( compare (a) and (b) in Fig. 1) ?

score 10 · Answer 1 · answered May 10 '22 at 10:16

10

(i) You can use NearestNeighborGraph with the appropriate manually defined DistanceFunction. If that function gives you trouble, use AdjacencyGraph@Unitize@UnitStep@DistanceMatrix[points, DistanceFunction -> ...].

(ii) Use an appropriate manually defined EdgeShapeFunction.

Most of the work will be constructing the correct distance function and edge shape function, but those are more of a mathematical problem than a Mathematica one.

answered May 10 '22 at 10:16

Szabolcs

234,956
30
623
1,263

1

Thank you for your comment with directions. Did you look in the linked articles? I will be waiting for a constructive answer – user64494 May 10 '22 at 10:30
As I see, EdgeShapeFunction is not useful here at all. – user64494 May 10 '22 at 10:48
In mild words, the documentation to DistanceFunction (see (https://reference.wolfram.com/language/ref/DistanceFunction.html) is too poor. – user64494 May 10 '22 at 10:52
If you want to use a different shape for edges than a line, you can do that with EdgeShapeFunction. Either you do this, or you abandon Graphcompletely and draw the graph completely manually. I am not aware of any other option. So EdgeShapeFunction is the option to use. – Szabolcs May 10 '22 at 11:04
4

Don't look at the documentation of DistanceFunction, but the documentation of the function that you want to use it from, i.e. NearestNeighborGraph or DistanceMatrix (whichever you choose to work with). Also, please be specific about what you tried and where you got stuck. This seems like a fairly trivial problem to solve, other than having to look up / derive the formulas for the appropriate sampling of points on the Poincaré disk, the correct distance function, and the shape of "lines" on the disk. No, there won't be anything built-in for these. You need to do it yourself. – Szabolcs May 10 '22 at 11:06
5

So don't expect to use DistanceFunction -> "SomePredefinedValue". You need to define the function yourself. The same for edge shapes. – Szabolcs May 10 '22 at 11:07
1

Szabolcs (@ does not work.): Sorry, I don't need directions and references. I am not a student and you are not my professor. Constructive suggestions are welcome. Do you understand me? – user64494 May 10 '22 at 13:58
8

I gave you constructive suggestions, and outlined how to complete the task. But it seems that you are looking only for a ready-to-use solution instead of an explanation of how to do it? If you downvote answers written with a helpful intention, you can hardly expect people to help you. – Szabolcs May 10 '22 at 14:04
1

Szabolcs (@ does not work.): Compare with that question. – user64494 May 10 '22 at 14:24

score 10 · Answer 2 · answered Jun 09 '22 at 20:22

Szabolcs's suggestion was pretty straightforward to implement, and the math for the Poincaré disk is easy (for those who are familiar with it), so just for giggles, here's my take:

(* https://mathematica.stackexchange.com/a/115580 *)
poincareMetric[u_?VectorQ, v_?VectorQ] := 
        Abs[ArcCosh[1 + 2 SquaredEuclideanDistance[u, v]/((1 - u . u) (1 - v . v))]]
(* NURBS representation of a line on the Poincaré disk *)
poincareLine[{p1_, p2_}] := Module[{s = p1 . p2 - 1, tm = Transpose[{p2, p1}]},
        BSplineCurve[{p1, tm . ({p1 . p1, p2 . p2} - 1)/(2 s), p2}, 
                     SplineDegree -> 2, SplineKnots -> {0, 0, 0, 1, 1, 1}, 
                     SplineWeights -> {1, 1/Sqrt[1 + (Det[tm]/s)^2], 1}]]
With[{n = 200 (* number of points ),
      r = 3, ( hyperbolic radius of disk )
      h = 0.35 ( fraction of radius to consider drawing an edge )},
     BlockRandom[SeedRandom[42, Method -> "MersenneTwister"]; ( for reproducibility )
                 pts = Table[With[{t = RandomReal[]}, ( hint: derive the inverse CDF *)
                                  Sqrt[(t Sinh[r/2]^2)/(1 + t Sinh[r/2]^2)]]
                                  Normalize[RandomVariate[NormalDistribution[], 2]],
                             {n}]];
                 NearestNeighborGraph[pts, {All, h r}, 
                                      DistanceFunction -> poincareMetric, 
                                      EdgeShapeFunction -> (poincareLine[#1] &),
                                      PlotRange -> 1,
                                      Prolog -> {Directive[Opacity[1/2],
                                                           AbsoluteThickness[1]],
                                                 Circle[]}]]

random Poincaré graph

Here is a 3D version; figuring out the code for this is left as an exercise. — J. M.'s missing motivation, Jun 09 '22 at 20:30
Thank you for your attempt to answer the question. Unfortunately, this is not it. If you read https://en.wikipedia.org/wiki/Poincaré_disk_model , you will know that "Hyperbolic straight lines consist of all arcs of Euclidean circles contained within the disk that are orthogonal to the boundary of the disk, plus all diameters of the disk" and " In the Poincaré disk model, lines in the plane are defined by portions of circles having equations of the form
$$ x^{2}+y^{2}+ax+by+1=0".$$ These are not represented as splines. BTW, your comments are too poor for an average Mathematica user. — user64494, Jun 10 '22 at 04:34
Had you been open-minded and more receptive to learning things, you would have tried to find out that circle arcs are representable as NURBS curves, and they can degenerate to straight lines if the weights are chosen appropriately. Well, I am not your professor, you are not my student, and this was just my way of having fun. I have no need to talk further if I don't feel a conversation is productive. — J. M.'s missing motivation, Jun 10 '22 at 05:08
@user64494 user64494 always make unreasonable demand about all of the answer. So I decided to never answer his question although I have know the answer. — cvgmt, Jun 10 '22 at 10:33
@user64494 Not your TA but here is Chapter 7: Conics and Circles from The NURBS Book. — Silvia, Jul 18 '22 at 13:50

Random graphs in Poincare disk

2 Answers2

Linked