My ultimate question: given data, what function is Interpolation with Method->"Spline" creating?
I recall from my graduate Numerical Analysis class years ago that piecewise spline interpolating functions had certain nice properties. The classic construction of natural splines can be found on Wolfram MathWorld here.
A colleague gave me some chemistry-related data and wanted to fit it with a smooth interpolating function. I was frustrated with how seemingly difficult this was to do with Mathematica. Googling "Mathematica spline interpolation" likely takes one to the MathWorld page above, or to obsolete functions like SplineFit, described here.
I found Interpolation, but for some reason the default settings don't produce a smooth curve. (Isn't that a natural desire?) The MathWorld page references BSplineCurve, which doesn't naturally compute an interpolating function, though the dedicated reader will find an example of interpolation if they read to "Applications/Interpolation" which requires the use of additional, unexplained code to compute knots.
After I computed my own natural cubic spline of the data, I found that Interpolation has a Method option where "Possible settings include "Spline" for spline interpolation...".
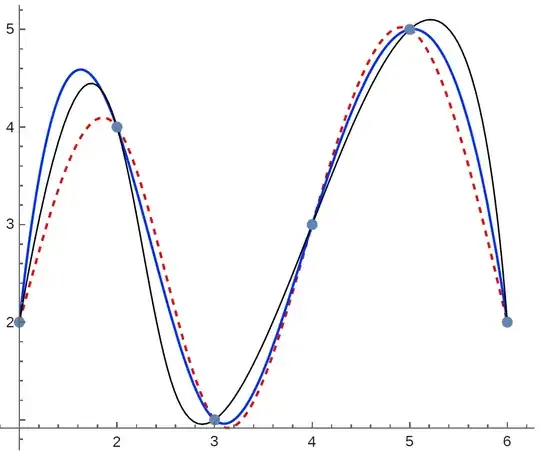
All three methods of computing a smooth interpolating "spline" produce different results. With the sample data set pts={{1,2},{2,4},{3,1},{4,3},{5,5},{6,2}}, the blue curve is produced with Interpolation[pts, Method->"Spline", InterpolationOrder->3], the black curve is produced using BSplineCurve and the documentation's Interpolation example, and the red, dashed curve is the classic natural spline per the MathWorld algorithm.
Again, my primary question is: what function is Interpolation with Method->Spline computing? A secondary question would be "Why doesn't Mathematica have a built-in natural spline creating function?
Edit: The BSplineCurve code, taken from the documentation:
dist = Accumulate[Table[EuclideanDistance[pts[[i]], pts[[i+1]]], {i, Length[pts]-1}]];
param = N[Prepend[dist/Last[dist], 0]];
knots = {0, 0, 0, 0,1/3, 2/3, 1, 1, 1, 1};
m = Table[BSplineBasis[{3, knots}, j - 1, param[[i]]], {i, 6}, {j, 6}];
ctrlpts = LinearSolve[m, pts];
Graphics[BSplineCurve[ctrlpts]]
Also, my cubic spline code isn't concise and isn't worth sharing, but I can confirm it produces the same function as ResourceFunction["CubicSplineInterpolation"][pts,"Natural"], as suggested in the comment.

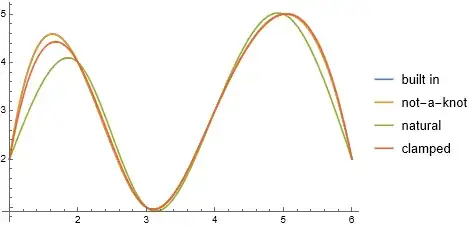
CubicSplineInterpolation. It has options for natural, clamped, not-a-knot flavors of cubic splines, and it returns anInterpolatingFunction– MarcoB May 16 '22 at 00:35CubicSplineInterpolationResourceFunctiondoes what I want. I stumbled on it as I was researching this question, though didn't try it. I don't understand the role of these resource functions; they seem like user-contributed functions, correct? They don't seem like a regular part of the Wolfram Language. – GregH May 16 '22 at 00:52AkimaSplineorAkimaInterpolation. – CA Trevillian May 16 '22 at 01:20csapi(x, y). – Michael E2 May 16 '22 at 01:48