How to solve 2D eigenvalue problem with robin boundary conditions

Question

I need to solve an eigenvalue problem in 2D as seen in the picture.

I've tried the function NDEigensystem but reading its documentation it seems it has issues with non-homogeneous boundary conditions. As solution I need the eigenvalues and eigenfunctions.

I would be very thankful if anybody could suggest how to solve such eigenvalue problem.

Answer 1

Let me extend my comments to an answer.

…it seems it has issues with non-homogeneous boundary conditions

Yes, but your b.c.s are homogeneous. NeumannValue can handle it, and we can use my allowfemdbc to automatically convert the b.c.s involving derivative to NeumannValue:

With[{u = u[x, y]}, lhs = Laplacian[u, {x, y}];
  bc = {u == 0 /. {{x -> -1}, {y -> -1}},
    {2 D[u, x] + u == 0 /. x -> 1,
     D[u, y] + u == 0 /. y -> 1}}];
tst = allowfemdbc[
   NDEigensystem[{lhs, bc} // Flatten, u, {x, -1, 1}, {y, -1, 1}, 4, 
    Method -> {"PDEDiscretization" -> {"FiniteElement", 
        "MeshOptions" -> {"MaxCellMeasure" -> 0.01}}}]]
(* {{0.916814, -4.13089, -4.56846, -9.61616}, …} *)
Plot3D[tst[[2, 1]][x, y], {x, -1, 1}, {y, -1, 1}]

Let's check if the Robin b.c.s are satisfied:

index = 2;
mid = Subtract @@@ bc[[2, 1]] /. u -> tst[[2, index]]; 
mid2 = Subtract @@@ bc[[2, 2]] /. u -> tst[[2, index]];
Plot[mid2, {x, -1, 1}, PlotRange -> All] ~Show~Plot[mid, {y, -1, 1}] 

Not bad, and will be better if MaxCellMeasure is smaller. The following is obtained with "MaxCellMeasure" -> 0.001:

Answer 2

Unfortunately NDEigensystem doesn't evaluate. Perhaps NDSolveValue helps to describe the system with Robin boundaries and gives an idea about the shape of the eigenfunction:

\[Lambda] = 1;
U = NDSolveValue[{Laplacian[u[x, y], {x, y}] - \[Lambda] u[x, y] ==
NeumannValue[- 1/2 u[x, y], x == 1] +NeumannValue[-  u[x, y], y == 1] , u[-1, y] ==$MachineEpsilon,u[x, -1 ] == $MachineEpsilon}, u,Element[{x, y}, Rectangle[{-1, -1}, {1, 1}]]]
Plot3D[U[x, y], Element[{x, y}, Rectangle[{-1,-1}, {1, 1}]]]

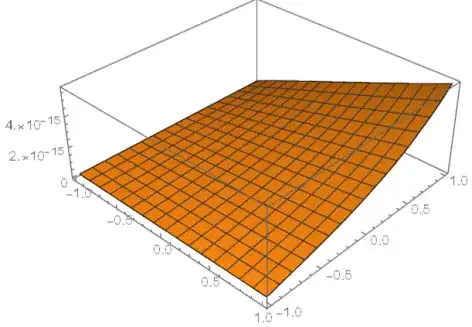
It looks like the problem has only trivial solution u==0 (Separation of variables might show this result analytically)!

addendum NDEigensystem works after all (thanks @xzczd's comments!)

es = NDEigensystem[{Laplacian[u[x, y], {x, y}] - 
    NeumannValue[-1/2 u[x, y], x == 1] - 
    NeumannValue[-u[x, y], y == 1], u[-1, y] == 0, u[x, -1] == 0}, u, 
  Element[{x, y}, Rectangle[{-1, -1}, {1, 1}]], 3]
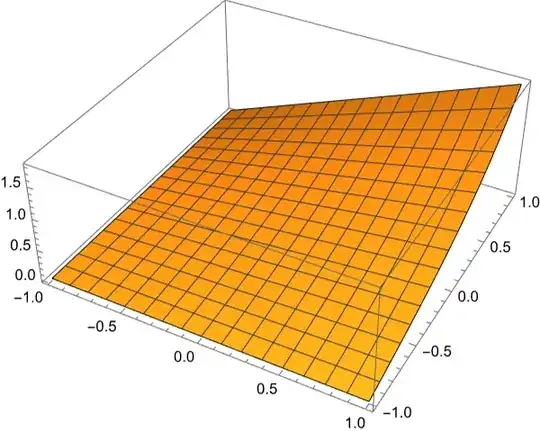
Map[Plot3D[#[x, y], Element[{x, y},Rectangle[{-1, -1}, {1, 1}]]] &,es[[2]]]