How to fix vertexnormals to eliminate a little shadow on the sphere?

Question

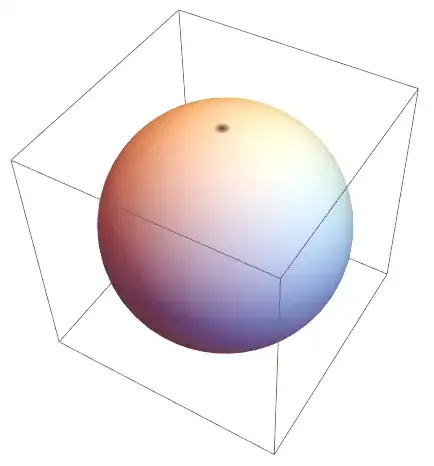
I am using the method here to draw a sphere, if VertexNormals is set, there will be a little shadow on the top of the ball. I'm not familiar with VertexNormals' calculations. Can we repair this defect?

vertNormals[vl_ /; ArrayQ[vl, 3, NumericQ]] := 
Block[{mdu, mdv, msh},
 msh = ArrayPad[#, {{1, 1}, {1, 1}}, "Extrapolated", InterpolationOrder -> 2] & /@ Transpose[vl, {2, 3, 1}];
 mdu = (ListCorrelate[{{1, 0, -1}}/2, #, {{-2, 1}, {2, -1}}, 0] & ) /@ msh;
 mdv = (ListCorrelate[{{-1}, {0}, {1}}/2, #, {{1, -2}, {-1, 2}}, 0] & ) /@ msh; 
 MapThread[Normalize @* Cross, Transpose[{mdu, mdv}, {1, 4, 2, 3}], 2]
 ];
MakePolygons[vl_/;ArrayQ[vl,3,NumericQ],OptionsPattern[{"Normals"->True}]]:=
Module[{dims=Most[Dimensions[vl]]},
GraphicsComplex[Apply[Join,vl],
Polygon[Flatten[Apply[Join[Reverse[#],#2]&,
Partition[Partition[Range[Times@@dims],Last[dims]],{2,2},{1,1}],{2}],1]],
If[TrueQ[OptionValue["Normals"]/.Automatic->True],
VertexNormals->Apply[Join,vertNormals[vl]],Unevaluated[]]]
];
list = Table[{Sin[θ]Cos[φ], Sin[θ]Sin[φ], Cos[θ]}, {θ, 0., Pi, Pi/50}, {φ, 0., 2Pi, 2Pi/50}];
Graphics3D[{EdgeForm[], MakePolygons[list, "Normals" -> True]}]

Related Links:
Polygon mesh: Compute vertex normals for smooth shading https://resources.wolframcloud.com/FunctionRepository/resources/PointArrayToPolygons/

Michael E2 · Accepted Answer · 2022-05-23T16:21:15.160

Use {θ, Subdivide[0.0001, Pi - 0.0001, 51]} instead of {θ, 0., Pi, Pi/50} to avoid the singularities in spherical coordinates. The normals end up being {0., 0., 0.} at the north pole, because the first row of the array list consists of all the same points:

(*  {{0., 0., 1.}, {0., 0., 1.}, ..., {0., 0., 1.}}  *)

A similar problem occurs at the south pole, except round-off error makes the points slightly different from each other. The normals at all the points around the south pole point only in approximately the same direction due to round-off error in differences computed by ListCorrelate[]. This causes some shading of the surface for me while I rotate the sphere with the mouse. When I release the mouse, the dark spot magically disappears.

But for a sphere centered at the origin, the vertex normals are the same as the position vectors of the points. You can use the original iterator {θ, 0., Pi, Pi/50} and get a good plot with the following:

Graphics3D[{EdgeForm[],
  MakePolygons[list, "Normals" -> False] /. 
   GraphicsComplex[pts_, g_, opts___] :> 
    GraphicsComplex[pts, g, VertexNormals -> pts, opts]
  }]

How to fix vertexnormals to eliminate a little shadow on the sphere?

1 Answers1