Finding poles of a function

Question

Is there a command to find the poles of a function $f=f(z)$?

example: let $$f(z) = \frac{1}{z^2-1}$$ then we know that the poles are at $z=\pm 1$ but is there a special command in mathematica to do this?

OK I thought there was some special command like Pole[f,z] or similar. Thanks, I'll try that. — mapel, Jun 12 '13 at 15:40
Or, if you want to handle things like Tan[]: Reduce[1/Tan[x] == 0, x]]. Should work nicely for rational functions, too. — J. M.'s missing motivation, Jun 12 '13 at 15:43
It really depends. If you're dealing with rational functions only, use Solve[], as @Michael recommended. Reduce[] takes a bit more effort internally... — J. M.'s missing motivation, Jun 12 '13 at 15:55
sometimes I use Solve[Denominator[f[z]]==0,z], but I would say this question is good because I also expect something much easier and more automatic (in case one doesn't want to organize the expression of f[z]). — Leo Fang, Jun 12 '13 at 16:31
In 13 version of Mathematica you can just use FunctionPoles experemental function! https://reference.wolframcloud.com/language/ref/FunctionPoles.html — Валерий Заподовников, Jan 05 '22 at 08:13

bill s · Answer 1 · 2013-06-12T16:48:25.277

14

There is a special function for this: it's called TransferFunctionPoles. For the case you asked for:

TransferFunctionPoles[TransferFunctionModel[{{1/(z^2 - 1)}}, z]]

which returns the expected answer that there are two poles at

{{{-1, 1}}}

TransferFunctionPoles can also handle multivariable input/output models of the kind that control engineers like to play with, including symbolic transfer functions and time-delay systems. There are a number of related commands including TransferFunctionZeros, TransferFunctionModel, StateSpaceModel ways of converting continuous to discrete models, and special plotting functions like RootLocusPlot and NyquistPlot.

edited Jun 12 '13 at 16:48

answered Jun 12 '13 at 16:28

bill s

68,936
4
101
191

5

It doesn't work with Tan[z]. It complains about polynomial numerators and denominators. Is this method restricted to rational functions? – Michael E2 Jun 12 '13 at 17:18
5

@@Michael E2 -- Whenever you see the phrase "transfer function," it implies rational functions. – bill s Jun 12 '13 at 18:12

score 4 · Answer 2 · answered Oct 31 '23 at 08:49

Since V 13.0 we have FunctionPoles:"

From the documentation: "FunctionPoles returns a list of pairs {pole, multiplicity}."

f = 1 / (z^2 - 1);
FunctionPoles[f, z]

{{-1, 1}, {1, 1}}

To only get the poles:

{a, b} = FunctionPoles[f, z][[All, 1]]

{-1, 1}

Plot[f, {z, -10, 10},
 Epilog -> {Red, Dashed, InfiniteLine[{a, 0}, {0, 1}], InfiniteLine[{b, 0}, {0, 1}]},
 PlotRange -> Automatic]

score 2 · Answer 3 · answered Jul 13 '18 at 00:10

Use FunctionDomain to find the real domain, then remove the whole line from the domain found. What is left are the poles. (this is all on the real line)

ClearAll[f,z]
f         = 1/(z^2-1)
domain    = FunctionDomain[f,z,Reals];
wholeLine = -Infinity < z < Infinity;

Reduce[ wholeLine && Not[domain],z,Reals]

Mathematica graphics

f         = Tan[z];
domain    = FunctionDomain[f,z,Reals];
wholeLine = -Infinity<z<Infinity;

Reduce[ wholeLine && Not[domain],z,Reals]

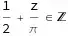
Mathematica graphics

It works for 2D also

ClearAll[f,x,y]
f         = 1/x Log[y];
domain    = FunctionDomain[f,{x,y},Reals];
wholeLine = {-Infinity<x<Infinity && -Infinity<y<Infinity};

Reduce[Join[wholeLine,{Not[domain]}],{x,y},Reals]

Mathematica graphics

In 13 FunctionPoles... – Валерий Заподовников Jan 05 '22 at 08:16 — Валерий Заподовников, Jan 05 '22 at 08:16

Finding poles of a function

3 Answers3

Linked