mathematica unduloid and nodoid plotting

Question

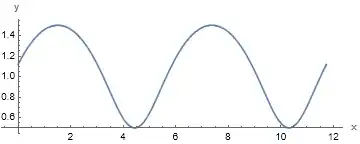
is there anyone who can help me plot this? I am currently using Wolfram Cloud but it doesn't allow me to plot these codes. I would really appreciate it. Thank you!

y[s_, B_] := (1 + B*B + 2*B*Sin[s]) ^(1/2) 
x[s_, B_] := Integrate [(1 + B*Sin[t] )/y [ t , B] , { t , 0, s}]
undulary = ParametricPlot[{x[s, 0.5 ], y [s , 0.5 ]}, { s , 0, 4*Pi}, PlotPoints -> 100]
Show[undulary, AxesLabel -> { "x ", "y "}, AspectRatio -> 1 /2.9 , PlotRange -> {0 , 4}]
y[s_] := (1 + 1/4 + Sin[s])^(1/2)
soli = NDSolve[{X'[s] == (1 + Sin[s]/2)/y[s] ,X[0]==0},{X}, {s , -4 Pi, 4 Pi}][[1]]
x[s_] := X[s] /.sol1;
c[s] = {x[s] , y[s]};
p2 = ParametricPlot3D[{x[s] , y[s]Cos[u], y[s]Sin[u]},
{s , 0, 3 Pi}, {u, Pi, 2 Pi},
PlotPoints->100, AspectRatio->Automatic,
Boxed->False, Axes->False]
y[s_, B_] := (1 + BB + 2BSin[s])^(1/2)
x[s_, B_] := Integrate[(1 + BSin[t])/y[t, B] , { t , 0, s}]
nodary = ParametricPlot[{x[s, 2], y[s, 2]}, {s , 0, 5*Pi},
AxesLabel ->{ "x ", "y"}, PlotPoints -> 100]
Show[nodary, AxesLabel -> { "x ", "y "} , AspectRatio -> 1 /1.9 ,
PlotRange -> {0 , 3.5}]
y[ s] := (1 + 4 + 4 Sin[s] )^(l/2 )
soi1 = NDSolvet{X'[s] == (1 + 2 Sin[s])/y [s] , X[0] == 0 }, {X },
{s , 0, 6 Pi}][[1]]
x[s_] := X[s] /.sol1;
c[s_] = {x[s], y [s]} ;
p2 = ParametricPlot3D [{x [s] , y[s] Cos[u], y[s] Sin[u]},
{s , 0, 5 Pi}, {u, Pi, 2 Pi}, PlotPoints -> 100,
AspectRatio -> Automatic, Boxed -> False,
Axes -> False]
p3 = ParametricPlot3D [{x [s] , y[s] Cos[u], y[s] Sin[u]},
{s , 0, 5 Pi}, {u, 0, 2 Pi}, PlotPoints->100,
AspectRatio->Automatic, Boxed -> False,
Axes -> False]

score 4 · Accepted Answer · answered Jun 08 '22 at 19:09

The equations from your version are messy, so instead I'll use the parametric equations for the Delaunay curve from here to construct the corresponding surface of revolution (that is, the unduloid corresponding to the elliptic Delaunay curve, and the nodoid corresponding to the hyperbolic Delaunay curve):

(* unduloid *)
With[{a = Sqrt[2], b = 1}, (* semiaxes of the generating ellipse *)
     ParametricPlot3D[{b EllipticE[t, 1 - a^2/b^2] -
                       Sqrt[((a^2 - b^2) (a - Sqrt[a^2 - b^2] Cos[t]))/
                            (a + Sqrt[a^2 - b^2] Cos[t])] Sin[t], 
                       b Sqrt[(a - Sqrt[a^2 - b^2] Cos[t])/
                              (a + Sqrt[a^2 - b^2] Cos[t])] Cos[u], 
                       b Sqrt[(a - Sqrt[a^2 - b^2] Cos[t])/
                              (a + Sqrt[a^2 - b^2] Cos[t])] Sin[u]},
                      {t, 0, 4 π}, {u, -π, π/2}]]

unduloid

(* nodoid *)
With[{a = 1, b = 1}, (* semiaxes of the generating hyperbola *)
     ParametricPlot3D[{b EllipticE[t, -(a^2/b^2)] - b EllipticF[t, -(a^2/b^2)] - 
                       a Sqrt[(Sqrt[a^2 + b^2] - a Cos[t])/
                              (Sqrt[a^2 + b^2] + a Cos[t])] Sin[t], 
                       b Sqrt[(Sqrt[a^2 + b^2] - a Cos[t])/
                              (Sqrt[a^2 + b^2] + a Cos[t])] Cos[u], 
                       b Sqrt[(Sqrt[a^2 + b^2] - a Cos[t])/
                              (Sqrt[a^2 + b^2] + a Cos[t])] Sin[u]},
                      {t, 0, 4 π}, {u, -π, π/2}]]

nodoid

score 3 · Answer 2 · answered Jun 08 '22 at 19:37

J.M.'s approach is much preferable, but your code can be easily improved:

Use numerical integration (NIntegrate) rather than attempting symbolic integration at every step (Integrate). See this FAQ for the reason why I added NumericQ to the definition of $x$.
You don't need to use 100 PlotPoints: that's painfully slow and it does not improved the quality much.
You also don't need to use Show: you can include all the options you need directly inside the ParametricPlot call.

ClearAll[x, y]
y[s_, B_] := (1 + B*B + 2*B*Sin[s])^(1/2)
x[s_?NumericQ, B_?NumericQ] := NIntegrate[(1 + B*Sin[t])/y[t, B], {t, 0, s}]
undulary = 
 ParametricPlot[
   {x[s, 1/2], y[s, 1/2]},
   {s, 0, 4*Pi}, 
   AxesLabel -> {"x ", "y "}, AspectRatio -> 1/3
 ]

nodary = 
 ParametricPlot[
   {x[s, 2], y[s, 2]}, 
   {s, 0, 5*Pi}, 
   AxesLabel -> {"x ", "y"}, AspectRatio -> 1/2
 ]

mathematica unduloid and nodoid plotting

2 Answers2