Calligraphic Pen Signature, Part II

Question

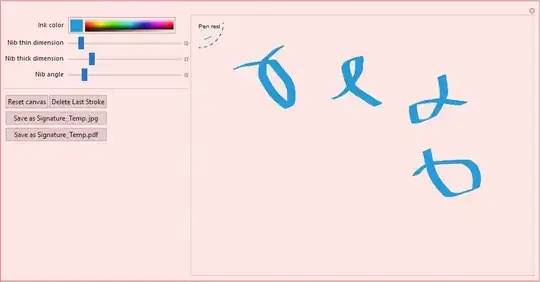
Continuing toward my goal pf getting a calligraphic signature pane pursuant to this answer (https://mathematica.stackexchange.com/a/13376/43662). I have produced the code below. The user writes using the mouse with the button held down. Subsequent presses produce new lines. Color and pen shape and angle are chosen.

Update

I am trying to combine with BSplineFunction in order to smoothen the angles and make the curves flow more evenly. It is better but can be improved.

The code for the angular panel:

mouseHandler := Block[{},
  (pos = MousePosition["Graphics"];
   btn = CurrentValue[{"MouseButtonTest", 1}];
   If[btn, (
     If[pos =!= None, AppendTo[posList[maxLine], pos]];
     posList[maxLine] = DeleteDuplicates@posList[maxLine];),
    (*else increment line counter and max line counter*)
    If[Length@posList[maxLine] > 3,
     maxLine++]];
   If[maxLine == 100, Break];
   )]
calligraphicLine[pts_List, baseThickness_, maxThickness_, 
  direction_] := ({Thickness[(Abs@
          Sin[Mod[ArcTan @@ Subtract @@ # + direction, 2 Pi]])*
        maxThickness + baseThickness], Line[#]} & /@ 
   Partition[pts, 2, 1])
Table[posList[i] = {}, {i, 100}];
posList[1] = Table[{-10 - i, -i}, {i, 4}]; maxLine = 1;
colr = RGBColor[0., 0.5, 0.9];
thinX = .001; thickX = .015; angle = 5.48;
Column[{Row@{
    ColorSlider[Dynamic[colr]],
    Column[{"\tNib Thin Dimension\t" Slider[
        Dynamic[thinX], {0.0001, .01}],
      "\tNib Thick dimenson\t" Slider[Dynamic[thickX], {.01, .025}],
      "\tNib Angle\t\t\t" Slider[Dynamic[angle], {0, 2 Pi}]}]
    },
  Dynamic[Graphics[{colr, Dynamic@Table[
       calligraphicLine[posList[i], thinX, thickX, angle]
       , {i, maxLine}],
     Black
     ,(*Dynamic@*)Table[
      Point[posList[i]]
      , {i, maxLine}]
     }, Frame -> False, FrameTicks -> False,
    AspectRatio -> Automatic,
    ImageSize -> Large, PlotRange -> {{-3, 3}, {-2, 2}}]]
  }]
Dynamic[mouseHandler]

To get the smoother lines, I follow it with

Show@Table[
  ParametricPlot[BSplineFunction[posList[i], SplineDegree -> 5][t]
    , {t, 0, 1}, PlotPoints -> 4 60, PlotRange -> {{-3, 3}, {-2, 2}}, 
    PlotStyle -> colr, Axes -> False] /. 
   Line[pts_] :> calligraphicLine[pts, thinX, thickX, angle]
  , {i, 2, maxLine - 1}]

For example, panel one and two might be, panel one:

and panel two:

The ends have blotches and the curves, while better, are not realistic.

@QuantumDot Yes, I do not know how or why one would think about changing the nib angle midstroke or between strokes. — Nicholas G, Jun 10 '22 at 01:47

Nicholas G · Accepted Answer · 2022-06-15T03:57:38.043

A proposed solution:

Manipulate[
 (Show[{(gr =
      Graphics[
       If[lineEx < 2, 
        White, {nibColor, 
         Table[With[{i = i}, 
           calligraphicLine[smoothedPoints[posList[i]], nibThinDim, 
            nibThickDim, nibAngle]], {i, Max[0, lineEx - 1]}]}], 
       PlotRange -> {{-2, 2}, {-1.5, 1.5}}, ImageSize -> Large])
    , Graphics[{nibColor,
      Dynamic[
       Block[{
         mousePos = 
          MousePosition[{"Graphics", Graphics}, 
           deftMsPos = {-1.89, 1.32}],
         mouseBtn = CurrentValue[{"MouseButtonTest", 1}],
         line = lineEx}, {
         locatorRectangle[mousePos, nibThinDim, nibThickDim, nibAngle],
         If[mouseBtn,
          (If[mousePos =!= None && mousePos != deftMsPos, 
            AppendTo[posList[line], mousePos]];
           calligraphicLine[posList[line], nibThinDim, nibThickDim, 
            nibAngle]),
          If[Length[posList[line]] > 3, line++; lineEx++;
           If[lineEx > 100, Break[]]]]}]],
      Black, Dashing[.01], Circle[{-2, 1.5}, .3],
      Text["Pen rest", {-2, 1.5}, {-1, 1}]
      }, PlotRange -> {{-2, 2}, {-1.5, 1.5}}, ImageSize -> Large]
    }])
 ,
 {{nibColor, RGBColor[0., 0.6, 0.8], 
   "Ink color"}, Black, Control -> ColorSlider},
 {{nibThinDim, .01, "Nib thin dimension"}, .0001, .1},
 {{nibThickDim, .1, "Nib thick dimension"}, .05, .3},
 {{nibAngle, RandomReal[{.35, .5}], "Nib angle"}, 0, \[Pi]},
 Delimiter,
 Column[{Row[{
     Button[
      "Reset canvas", {Table[posList[i] = {}, {i, 100}]; lineEx = 1}],
     Button[
      "Delete Last Stroke", {posList[lineEx - 1] = {}; 
       lineEx = lineEx - 1}]}],
   Button["Save as Signature_Temp.jpg", 
    Export[FileNameJoin[{$UserDocumentsDirectory, 
       "Signature_Temp.jpg"}], Show[gr, PlotRange -> All]]],
   Button["Save as Signature_Temp.pdf", 
    Export[FileNameJoin[{$UserDocumentsDirectory, 
       "Signature_Temp.pdf"}], Show[gr, PlotRange -> All]]]}]
 , ControlPlacement -> Left
 , Initialization :> {
   lineEx = 1,
   calligraphicLine[pts_List, thin_, thick_, angle_] := 
    Map[calLineComp[#[[1]], #[[2]], thin, thick, angle] &, 
     Partition[pts, 2, 1]],
   calLineComp[point1_, point2_, thin_, thick_, angle_] := Block[{
      p1lr = 
       point1 + {Cos[angle] (thick/2) + Sin[angle] (thin/2), 
         Sin[angle] (thick/2) - 
          Cos[angle] (thin/2)},(*lower right of point1*)
      p1ur = 
       point1 + {Cos[angle] (thick/2) - Sin[angle] (thin/2), 
         Sin[angle] (thick/2) + Cos[angle] (thin/2)},(*upper right*)
      p1ul = 
       point1 - {Cos[angle] (thick/2) + Sin[angle] (thin/2), 
         Sin[angle] (thick/2) - Cos[angle] (thin/2)},
      p1ll = 
       point1 - {Cos[angle] (thick/2) - Sin[angle] (thin/2), 
         Sin[angle] (thick/2) + Cos[angle] (thin/2)},
      p2lr = 
       point2 + {Cos[angle] (thick/2) + Sin[angle] (thin/2), 
         Sin[angle] (thick/2) - Cos[angle] (thin/2)},
      p2ur = 
       point2 + {Cos[angle] (thick/2) - Sin[angle] (thin/2), 
         Sin[angle] (thick/2) + Cos[angle] (thin/2)},
      p2ul = 
       point2 - {Cos[angle] (thick/2) + Sin[angle] (thin/2), 
         Sin[angle] (thick/2) - Cos[angle] (thin/2)},
      p2ll = 
       point2 - {Cos[angle] (thick/2) - Sin[angle] (thin/2), 
         Sin[angle] (thick/2) + Cos[angle] (thin/2)}},
     {
      Polygon[{p1lr, p1ur, p1ul, p1ll}],(*starting poly*)
      Polygon[{p2lr, p2ur, p2ul, p2ll}],(*ending poly*)
      Polygon[{p1lr, p2lr, p2ur, p1ur}],(*polys connecting each side*)
      Polygon[{p1ur, p2ur, p2ul, p1ul}], 
      Polygon[{p1ul, p2ul, p2ll, p1ll}], 
      Polygon[{p1ll, p2ll, p2lr, p1lr}]}],
   locatorRectangle[point_, thin_, thick_, angle_] := 
    Polygon[{point + {Cos[angle] (thick/2) + Sin[angle] (thin/2), 
        Sin[angle] (thick/2) - Cos[angle] (thin/2)},
      point + {Cos[angle] (thick/2) - Sin[angle] (thin/2), 
        Sin[angle] (thick/2) + Cos[angle] (thin/2)},
      point - {Cos[angle] (thick/2) + Sin[angle] (thin/2), 
        Sin[angle] (thick/2) - Cos[angle] (thin/2)},
      point - {Cos[angle] (thick/2) - Sin[angle] (thin/2), 
        Sin[angle] (thick/2) + Cos[angle] (thin/2)}}],
   smoothedPoints[pts_List] := 
    smoothedPoints[pts] = 
     Table[BSplineFunction[pts][t], {t, 0, 1, 0.005}],
   Table[posList[i] = {}, {i, 100}]
   }]

An example:

Calligraphic Pen Signature, Part II

1 Answers1