Plotting rainbow circle

Question

I am trying to plot a parametric circle in rainbow colors. It should go round once, but I'd like to be able to make it go round the rainbow an arbitrary amount of times.

I currently have:

ParametricPlot3D[{Sin[u] Sin[Theta], Cos[u] Sin[Theta], 
  Cos[Theta]} /. Theta -> Pi/6, {u, -Pi, Pi}, 
  PlotStyle -> Directive[Thickness[.01]], 
  ColorFunction -> Function[{x, y, z}, ColorData["Rainbow"][(Arg[x + I y] + Pi)/(2 Pi)]]]

Which I think should choose a color from the ColorData named Rainbow (which changes only between 0 and 1 (the result of Arg lies between -Pi and Pi, so adding Pi and dividing the resulting interval by 2 Pi will give me a number between 0 and 1) depending on the angle of the circle. I get an almost decent result if I divide by Pi/2 instead of 2 Pi: Nearly rainbow circle

But I have no idea why there is yellow and green twice. I'm certainly missing something, does anyone know what?

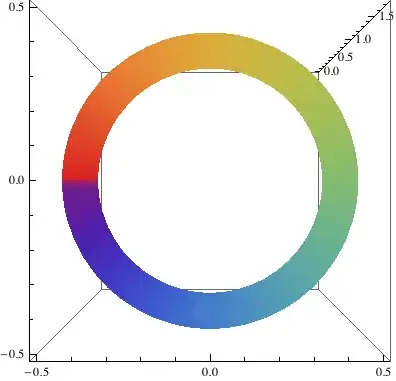
@J. M. Adding ColorFunctionScaling->False "fixes" it. But why would it being set to True mess up my own scaled values? — rubenvb, Jun 13 '13 at 13:37
If you look at the docs, you'll see that with the setting ColorFunctionScaling -> True, the x and y are scaled even before being fed to your color function; that's different from scaling Arg[], the output. — J. M.'s missing motivation, Jun 13 '13 at 13:42

score 3 · Answer 1 · answered Jun 13 '13 at 13:51

Since you're providing the scaling, you don't want Mathematica to do it, so

ParametricPlot3D[{Sin[u] Sin[Theta], Cos[u] Sin[Theta], Cos[Theta]} /. Theta -> Pi/6, 
   {u, -Pi, Pi}, 
   PlotStyle -> Directive[Thickness[.1]], 
   ColorFunction -> 
     Function[{x, y, z}, ColorData["Rainbow"][(Arg[x + I y] + Pi)/(2 Pi)]],
   ColorFunctionScaling -> False]

enter image description here

score 1 · Answer 2 · answered Jun 13 '13 at 14:03

Building on m_goldberg's answer, you can also use Hue instead of Rainbow -- this provides brighter colors and is still pretty much around the rainbow.

ParametricPlot3D[{Sin[u] Sin[Theta], Cos[u] Sin[Theta], 
             Cos[Theta]} /. Theta -> Pi/6, {u, -Pi, Pi}, 
         PlotStyle -> Directive[Thickness[.1]], 
         ColorFunction -> Function[{x, y, z}, Hue[(Arg[x + I y] + Pi)/(2 Pi)]], 
         ColorFunctionScaling -> False, Boxed -> False, Axes -> False]

enter image description here

Plotting rainbow circle

2 Answers2