While it's unclear which of the following is the desired form, I'll give a general approach and then some specific alternatives:
f[x1_, x2_,..., x100_] := ... (* coordinates as separate arguments *)
f[{x1_, x2_,..., x100_}] := ... (* coordinates in a single vector *)
First interpretation
I interpret the exclamation, "It's inefficient!", to mean it's inefficient to type. Thus we seek an efficient way to edit. Some code-construction together with copy and paste is helpful.
First construct our arguments. We can apply our func to get code that is ready to edit and add our definition := .... We can then apply our next function to args and edit the output to construct another function. It seems efficient to me.
ClearAll["x*", func]; (* make the workspace ready *)
args = Table[Pattern[Evaluate@ToExpression["x" <> ToString@n], _],
{n, 100; 3}]
func @@ args
func @ args
(*
{x1_, x2_, x3_}
func[x1_, x2_, x3_]
func[{x1_, x2_, x3_}]
*)
Alternatively, depending on the desired form, one can copy the output of args, or one can delete the { and } from the output of args. In either case, one gets a cell that can be copied and pasted into a function definition.
So I don't see any inefficiency in constructing the left-hand side of the definition. The formula for right-hand side, in terms of a hundred variables, might be horrible, but that's beside the point, I guess.
Second interpretation
I can see three possible options: We could want the first form (like in @lericr's answer currently accepted), the second form (like in the OP's answer), or both forms to work. In my early days of using Mathematica, I became irritated that functions $f : {\bf R}^3 \rightarrow {\bf R}$ might equally be considered a function of a single point $(x,y,z)$ or a function of three independent variables $x$, $y$, and $z$. It makes a difference to Mathematica, but not to mathematicians. So I got in the habit of doing both, as seen in the examples func1 and func2. The third, which uses an anonymous Function, cannot be polymorphic. The fourth could be made polymorphic in the same way func1 is; or one could use Apply@func4, which operator form of Apply did not exist in the early days.
The setup.
We set up the variables inside Hold[]. We also assign values to the variables to check that our definitions do not leak evaluations.
ClearAll["x*", func1, func2, func3, func3vec, func4];
vars = Flatten[
Hold @@
ToExpression[Table["x" <> ToString@n, {n, 3}], StandardForm,
Hold]];
{x1, x2, x3} = Prime@Range@3;
1, 2.
Note func1 evaluates the formula when passed the individual coordinate, and has a form for converting func1[vector] to func1[x1, x2, x3]. In func2 it's the reverse.
With[{nvars = Length@vars},
func1[x_List] /; Length@x == nvars := func1 @@ x;
Activate@Replace[vars, x_ :> Inactive[Pattern][x, _], 1] /.
Hold[v__] :>
(func1[v] := x1 + x2 + x3);
];
func2[x_List] := x . {1, 1, 1}; (* math. short-cut :) *)
func2[x___] := func2[{x}];
3.
An anonymous function can't be polymorphic, so different versions are given for each form. One could have func3vec call func3 conditionally, but that hardly seems a solution anyone would prefer.
vars /. Hold[v__] :>
(func3 = Function[{v}, x1 + x2 + x3])
(* Function[{x1, x2, x3}, x1 + x2 + x3] *)
vars /. Hold[v__] :>
(func3vec =
Block[{v},
{v} = #;
x1 + x2 + x3] &)
(* Block[{x1, x2, x3}, {x1, x2, x3} = #1; x1 + x2 + x3] & *)
4.
If one can construct the body of the function expr programmatically, then func4 shows a way to make it into a function. The function func4 can be overloaded to handle a vector argument in the same was that func1 was.
expr = vars /. Hold[v__] :> Block[{v}, (* make held expression *)
x1 + x2 + x3 // Hold[#] &]; (* for body of func4 *)
{Activate@Replace[vars, x_ :> Inactive[Pattern][x, _], 1],
expr} /.
{Hold[v__], Hold[e_]} :> (func4[v] := e);
Testing. Since func3 and func4 don't have a vector form, they can be applied to a vector argument with the operator form Apply@f.
Through[{func1, func2, Apply@func3, Apply@func4}[Table[x[n], {n, 3}]]]
(*
{x[1] + x[2] + x[3],
x[1] + x[2] + x[3],
x[1] + x[2] + x[3],
x[1] + x[2] + x[3]}
*)
Through[{func1, func2, func3, func4}[x[1], x[2], x[3]]]
(* <same as above> *)
func3vec@Table[x[n], {n, 3}] (* for completeness )
( x[1] + x[2] + x[3] *)
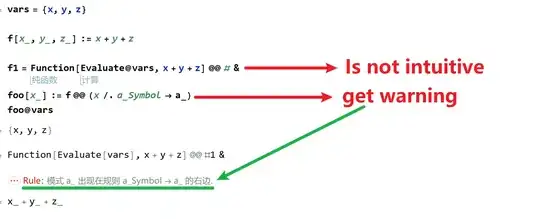

F[Thread[Pattern[Evaluate[vars], _]]] := something– chyanog Jun 22 '22 at 11:32f={x,y,z}|->x+y+z. – cvgmt Jun 22 '22 at 11:57g[list_] := Total[list]orh[list_] := Plus @@ list. This would modify the function calls tog[{x, y, z}]. It may also have the added advantage that variables in your function call can be grouped by function / logically, alleviating the chance of simple errors and improving readability. – MarcoB Jun 22 '22 at 12:00f[x_,y_,z_]orf[{x_,y_,z_}]? The first, which you say want, is not of the formf[vars], which you claim is equivalent. Rather the second is equivalent tof[vars]. So which do you want, the first or the second? – Michael E2 Jun 22 '22 at 14:53f[{x,y,z}]to evaluate tof[x,y,z]? Evaluating tof[x_,y_,z_]seems wrong, is certainly quite different fromf[{x,y,z}]. Notexandx_are different, andx_does not depend onx. – Michael E2 Jun 22 '22 at 16:46