How are the projections of this plot made?

Question

I want to make projections of a 3D plot as shown in this image .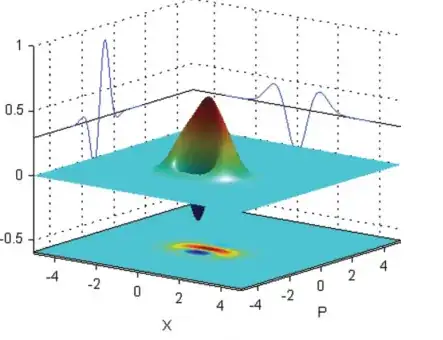

I took this image from this paper: Multiphoton state engineering by heralded interference between single photons and coherent states. I know how to make a 3D plot like this. I only want to know how these projections on the face grids were made. I tried making this by using the "projecttoWalls" function from this question: How to project 3d image in the planes xy, xz, yz? but it gives me a projection of my plot. Can anybody tell me how to draw projections like in the above image? (I get that these projections are like a 2D version of this plot but I don't know how to make them.)

This is the code of my 3D plot:

    w0 = (2*(7 - 20*I*Sqrt[2]*p - 24*p^2 - 20*Sqrt[2]*q + 48*I*p*q + 24*q^2 + 8*(-3 + 8*p^2 + 8*I*p*(Sqrt[2] - 2*q) + 8*Sqrt[2]*q - 8*q^2)*Conjugate[p]^2 + 
      4*(-5*Sqrt[2] + 16*Sqrt[2]*p^2 + 28*q - 16*Sqrt[2]*q^2 - 4*I*p*(-7 + 8*Sqrt[2]*q))*Conjugate[q] + 8*(3 - 8*p^2 - 8*I*p*(Sqrt[2] - 2*q) - 8*Sqrt[2]*q + 8*q^2)*Conjugate[q]^2 + 
      4*Conjugate[p]*(-16*I*Sqrt[2]*p^2 - 4*p*(-7 + 8*Sqrt[2]*q) + I*(5*Sqrt[2] - 28*q + 16*Sqrt[2]*q^2) - 4*(-8*I*p^2 + 8*p*(Sqrt[2] - 2*q) + I*(3 - 8*Sqrt[2]*q + 8*q^2))*Conjugate[q])))/
    E^(2*Abs[-(1/Sqrt[2]) + I*p + q]^2)/(3*Pi*(Sqrt[2] - 4*I*p - 4*q)*(Sqrt[2] + 4*I*Conjugate[p] - 4*Conjugate[q]));
p1 = Plot3D[w0, {q, -5, 5}, {p, -5, 5}, PlotRange -&gt; All];
p2 = DensityPlot[w0, {q, -5, 5}, {p, -5, 5}, PlotRange -&gt; All, Frame -&gt; False, PlotPoints -&gt; 90];
level = -0.4;
gr = Graphics3D[{Texture[p2], EdgeForm[], Polygon[{{-5, -5, level}, {5, -5, level}, {5, 5, level}, {-5, 5, level}}, 
 VertexTextureCoordinates -&gt; {{0, 0}, {1, 0}, {1, 1}, {0, 1}}]}, Lighting -&gt; &quot;Neutral&quot;];
f1 = Show[p1, gr, PlotRange -&gt; All, Boxed -&gt; False, Ticks -&gt; {Automatic, Automatic, None}];

Perhaps How to project 3d image in the planes xy, xz, yz? helps — Ulrich Neumann, Jun 28 '22 at 11:23
@UlrichNeumann No it does not help with this graph. I have mentioned it in the question as well. It creates projections but I want them like in the plot in my question. — Anaya, Jun 28 '22 at 11:30
Sorry, I didn't read your question in detail. From your image I cann't see what kind of projections you're looking for. Are these the outer contours of the 3D-plot? — Ulrich Neumann, Jun 28 '22 at 11:36
I am talking about the projections or waveforms on the gridded walls. Maybe these are not projections, but rather a 2D form of the 3D plot. I am sorry if I am not being clear:) — Anaya, Jun 28 '22 at 11:38
So do I! My question: How these projections depend on the 3D-Plot? — Ulrich Neumann, Jun 28 '22 at 11:41
Actually my supervisor showed me this plot and asked me to make my 3D plots like this but I coudn't understand either how they are related to the 3D plot. I am also confused. — Anaya, Jun 28 '22 at 11:43
From what I have understood by seeing the other plots in the paper: Multiphoton state engineering by heralded interference between single photons and coherent states, these projections are like a 2D version of showing the changes in the 3D plots. — Anaya, Jun 28 '22 at 11:49
There is an email to contact the authors on the paper, I would email them and ask what is depicted in the projections onto the walls of figs. 3,4. — N.J.Evans, Jun 28 '22 at 11:52
@UlrichNeumann Use this: Multiphoton state engineering by heralded interference between single photons and coherent states. — Anaya, Jun 28 '22 at 11:53
For what it's worth they look like plots of W(x,0), W(0,p) respectively. — N.J.Evans, Jun 28 '22 at 11:58
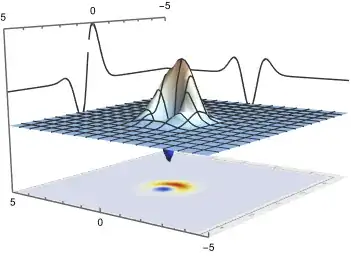
Looks like a slice of f(x,y) at some x say x=0. To get the slice on the left wall at myX=-5, I would use ParametricPlot3D[{-5,y,f(0,y)},{y,-5,5}]. Can you post the f(x,y) or some other similar f(x,y)? — josh, Jun 28 '22 at 12:09
@josh I have edited the function in my question and now w0 is almost like the function used to make the 3D plot in the figure. — Anaya, Jun 28 '22 at 13:19
@Anaya: Ok sorry. Didn't see that. Can't get to it now. Will work on it later if no one else posts. — josh, Jun 28 '22 at 14:07

score 7 · Accepted Answer · answered Jun 28 '22 at 15:15

Redefine your expression as a function of $p$ and $q$:

ClearAll[w0]
w0[p_, q_] := (2*(7 - 20*I*Sqrt[2]*p - 24*p^2 - 20*Sqrt[2]*q + 
        48*I*p*q + 24*q^2 + 
        8*(-3 + 8*p^2 + 8*I*p*(Sqrt[2] - 2*q) + 8*Sqrt[2]*q - 8*q^2)*
         Conjugate[p]^2 + 
        4*(-5*Sqrt[2] + 16*Sqrt[2]*p^2 + 28*q - 16*Sqrt[2]*q^2 - 
           4*I*p*(-7 + 8*Sqrt[2]*q))*Conjugate[q] + 
        8*(3 - 8*p^2 - 8*I*p*(Sqrt[2] - 2*q) - 8*Sqrt[2]*q + 8*q^2)*
         Conjugate[q]^2 + 
        4*Conjugate[
          p]*(-16*I*Sqrt[2]*p^2 - 4*p*(-7 + 8*Sqrt[2]*q) + 
           I*(5*Sqrt[2] - 28*q + 16*Sqrt[2]*q^2) - 
           4*(-8*I*p^2 + 8*p*(Sqrt[2] - 2*q) + 
              I*(3 - 8*Sqrt[2]*q + 8*q^2))*Conjugate[q])))/
    E^(2*Abs[-(1/Sqrt[2]) + I*p + q]^2)/(3*
     Pi*(Sqrt[2] - 4*I*p - 4*q)*(Sqrt[2] + 4*I*Conjugate[p] - 
       4*Conjugate[q]));

Generate the main plot and projections using ParametricPlot3D (I use a modification of a technique I learned in this answer):

ClearAll[full3D, xzplane, yzplane]
full3D[x_, y_] := {x, y, w0[x, y]}
xzplane[x_, y_] := {5, y, w0[0, y] + 0.15}
yzplane[x_, y_] := {x, -5, w0[x, 1] + 0.15}
pplot = ParametricPlot3D[
   {full3D[x, y], xzplane[x, y], yzplane[x, y]},
   {x, -5, 5}, {y, -5, 5},
   PlotRange -> All, PlotRangePadding -> None,
   ColorFunction -> "ThermometerColors",
   BoxRatios -> {1, 1, 2/3}
]

Then generate the DensityPlot and add it as a texture, as you did in your own code:

density = DensityPlot[
   w0[p, q], {p, -5, 5}, {q, -5, 5},
   PlotPoints -> 150,
   ColorFunction -> "TemperatureMap", PlotRange -> All
];
level = -0.3;
gr = Graphics3D[{
       Texture[p2], EdgeForm[], 
       Polygon[{{-5, -5, level}, {5, -5, level}, {5, 5, level}, {-5, 5, level}}, 
     VertexTextureCoordinates -> {{0, 0}, {1, 0}, {1, 1}, {0, 1}}]}, 
     Lighting -> "Neutral"];
Show[
  {pplot, gr},
  PlotRange -> All, Boxed -> False, 
  Ticks -> {Automatic, Automatic, None},
  ViewPoint -> {-2, 2.5, 0.5}, ViewVertical -> {-0.3, 0.3, 1}
]

Thank you so much! Moreover, for beginners like me working on a similar problem, using the command Exclusions->None inside the ParametricPlot3D command removes the break in the left projection. :) — Anaya, Jun 29 '22 at 05:29
Is there a way to remove the mesh and still have the parametric curves on the walls because when I use Mesh->None, my parametric curves disappear and only the 3D plot remains? — Anaya, Jun 29 '22 at 06:29

How are the projections of this plot made?

1 Answers1