0

Suppose I have some multidimensional function that is computationally very expensive to evaluate. Here, I will just use

ExpensiveFunction[x_] := 0.01*{3*x, -x^2, 0.1*x^3};

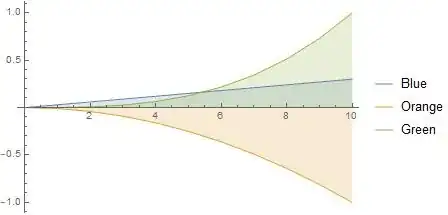
I want to make a discrete plot that looks like this:

DiscretePlot[
{ExpensiveFunction[x][[1]], ExpensiveFunction[x][[2]], ExpensiveFunction[x][[3]]}, 
{x, 0, 10, 1}, Joined -> True, PlotLegends -> {"Blue", "Orange", "Green"}]

DiscretePlot 1

However, I want to call ExpensiveFunction as few times as possible. Thus, I write equivalently (or so I thought):

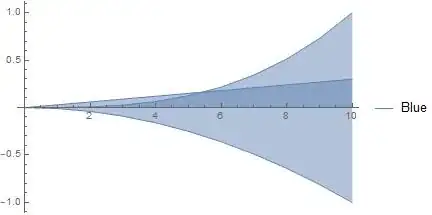
DiscretePlot[ExpensiveFunction[x],
{x, 0, 10, 1}, Joined -> True, PlotLegends -> {"Blue", "Orange", "Green"}]

Discrete Plot 2

Obviously, this is not the same, and the coloring and the labels are messed up.

I do not understand: Why is this not equivalent to the first plot? What is the difference between {ExpensiveFunction[x][[1]], ExpensiveFunction[x][[2]], ExpensiveFunction[x][[3]]} and ExpensiveFunction[x]? And how can I reproduce the first plot without calling ExpensiveFunction too often?

Andreas Tsevas
  • 133
  • 5
  • 4
    Use Evaluate. That is ExpensiveFunction[x_] = 0.01*{3*x, -x^2, 0.1*x^3}; DiscretePlot[ExpensiveFunction[x] // Evaluate, {x, 0, 10, 1}, Joined -> True, PlotLegends -> {"Blue", "Orange", "Green"}] – cvgmt Jun 29 '22 at 22:42
  • @cvgmt Wow, that works, thank you! But why does Evaluate make any difference here? It seems a bit counterintuituve to me that the same object is treated so differently depending on when exactly it is evaluated (either by Evaluate or by DiscretePlot). And also, why does my first plot behave so differently from the second one then? – Andreas Tsevas Jun 29 '22 at 22:49
  • 3
    Plotting functions such as DiscretePlot have the attribute HoldAll. Since the argument is initially held, it is seen as a single object. Using Evaluate forces immediate evaluation and the argument is seen as a list of three elements. – Bob Hanlon Jun 29 '22 at 22:53
  • @BobHanlon Thanks, that answers my questions! – Andreas Tsevas Jun 29 '22 at 22:56

0 Answers0