Layout improvements for planar graph

Question

I recently used Cage software to generate a 24-vertex planar graph. All details of the graph are as follows, including the coordinates of each of its vertices. I know it is 3-connected.

   1         2.055  -0.006        2  3  4  5
   2         1.902  -0.845        1  6  7  3
   3         1.3    -0.504        1  2  8  4
   4         1.3     0.497        1  3  8  5
   5         1.906   0.831        1  4  9  6
   6         3.272   0.003        2  5  10  11
   7         0.635  -1.656        2  11  12  8
   8         0.793  -0.002        3  7  9  4
   9         0.63    1.649        5  8  12  10
  10         0.163   3.111        6  9  13  14
  11         0.163  -3.106        6  14  15  7
  12         0.174  -0.004        7  15  13  9
  13        -0.291   1.674        10  12  16  17
  14        -2.946   0.003        10  17  18  11
  15        -0.29   -1.675        11  18  16  12
  16        -0.422   0.005        13  15  19  20
  17        -1.575   0.874        13  20  21  14
  18        -1.568  -0.868        14  21  19  15
  19        -0.876  -0.646        16  18  22  23
  20        -0.88    0.653        16  23  24  17
  21        -1.835   0.003        17  24  22  18
  22        -1.344  -0.3          19  21  24  23
  23        -0.92    0.004        19  22  24  20
  24        -1.347   0.306        20  23  22  21

So the first thing I considered was its Tutte embedding. Unfortunately it worked very poorly. So I tried the method provided in the link below.

• How to plot planar graphs in a visually pleasing way?

   g = Graph[{1 \[UndirectedEdge] 2, 1 \[UndirectedEdge] 3, 
  1 \[UndirectedEdge] 4, 1 \[UndirectedEdge] 5, 
  2 \[UndirectedEdge] 3, 2 \[UndirectedEdge] 6, 
  2 \[UndirectedEdge] 7, 3 \[UndirectedEdge] 4, 
  3 \[UndirectedEdge] 8, 4 \[UndirectedEdge] 5, 
  4 \[UndirectedEdge] 8, 5 \[UndirectedEdge] 6, 
  5 \[UndirectedEdge] 9, 6 \[UndirectedEdge] 10, 
  6 \[UndirectedEdge] 11, 7 \[UndirectedEdge] 8, 
  7 \[UndirectedEdge] 11, 7 \[UndirectedEdge] 12, 
  8 \[UndirectedEdge] 9, 9 \[UndirectedEdge] 10, 
  9 \[UndirectedEdge] 12, 10 \[UndirectedEdge] 13, 
  10 \[UndirectedEdge] 14, 11 \[UndirectedEdge] 14, 
  11 \[UndirectedEdge] 15, 12 \[UndirectedEdge] 13, 
  12 \[UndirectedEdge] 15, 13 \[UndirectedEdge] 16, 
  13 \[UndirectedEdge] 17, 14 \[UndirectedEdge] 17, 
  14 \[UndirectedEdge] 18, 15 \[UndirectedEdge] 16, 
  15 \[UndirectedEdge] 18, 16 \[UndirectedEdge] 19, 
  16 \[UndirectedEdge] 20, 17 \[UndirectedEdge] 20, 
  17 \[UndirectedEdge] 21, 18 \[UndirectedEdge] 19, 
  18 \[UndirectedEdge] 21, 19 \[UndirectedEdge] 22, 
  19 \[UndirectedEdge] 23, 20 \[UndirectedEdge] 23, 
  20 \[UndirectedEdge] 24, 21 \[UndirectedEdge] 22, 
  21 \[UndirectedEdge] 24, 22 \[UndirectedEdge] 23, 
  22 \[UndirectedEdge] 24, 23 \[UndirectedEdge] 24}]
  Manipulate[
    IGLayoutTutte[
     IGEdgeMap[(EuclideanDistance @@ #)^power &, 
      EdgeWeight -> IGEdgeVertexProp[VertexCoordinates], g], 
     VertexSize -> 1/2], {{power, 1}, 0.5, 3}]
  

No matter how we adjust it, there will always be some vertices crowded together.

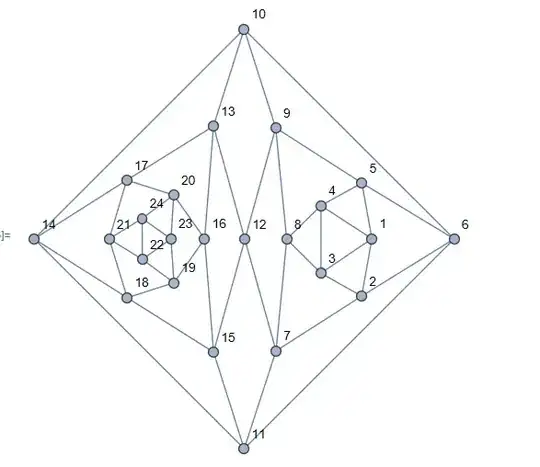
In the end, I used the original software's datas of coordinates of vertices. I found that it doesn't guarantee that every face is convex, but the layout is fine. So my question is, if I don't require that every face is convex, does Mathematica provide a good planar layout?

s = Graph[g, 
  VertexCoordinates -> {1 -> {2.055, 0.006}, 2 -> {1.902, -0.845},
    3 -> {1.3, -0.504}, 4 -> {1.3, 0.497}, 5 -> {1.906, 0.831}, 
    6 -> {3.272, 0.003}, 7 -> {0.635, -1.656}, 8 -> {0.793, -0.002}, 
    9 -> {0.63, 1.649}, 10 -> {0.163, 3.111}, 11 -> {0.163, -3.106}, 
    12 -> {0.174, -0.004}, 13 -> {-0.291, 1.674}, 
    14 -> {-2.946, 0.003}, 15 -> {-0.29, -1.675}, 
    16 -> {-0.422, 0.005}, 17 -> {-1.575, 0.874}, 
    18 -> {-1.568, -0.868}, 19 -> {-0.876, -0.646}, 
    20 -> {-0.88, 0.653}, 21 -> {-1.835, 0.003}, 22 -> {-1.344, -0.3},
     23 -> {-0.92, 0.004}, 24 -> {-1.347, 0.306}}, 
  VertexLabels -> All,VertexSize -> 0.3]

Answer 1

The trick with a power-transformation of edge weights will work much better if you choose a different face to be the outer face. Here's an example after choosing the same face that you show in your question.

How does one detect such a face? That would be an interesting question that I don't have the time to think about right now, unfortunately.

face = {10, 6, 11, 14};
Manipulate[
 IGLayoutTutte[
  IGEdgeMap[#^a &, EdgeWeight]@
   IGDistanceWeighted@IGLayoutTutte[g, "OuterFace" -> face],
  "OuterFace" -> face],
 {a, 0.5, 3}]

---

Update: A simple heuristic for choosing a nice face may be to take a face that corresponds to a low eccentricity vertex in the dual graph. For this graph, any of these faces work well:

In[63]:= IGFaces[g][[ GraphCenter@IGDualGraph[g] ]]
Out[63]= {{6, 10, 14, 11}, {7, 11, 15, 12}, {9, 12, 13, 10}, {10, 13, 
  17, 14}, {11, 14, 18, 15}, {12, 15, 16, 13}}