Visualizing action of matrix

Question

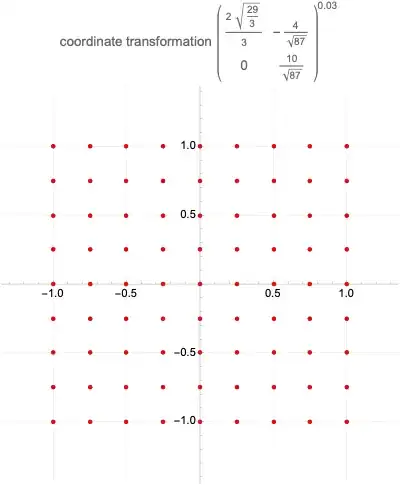
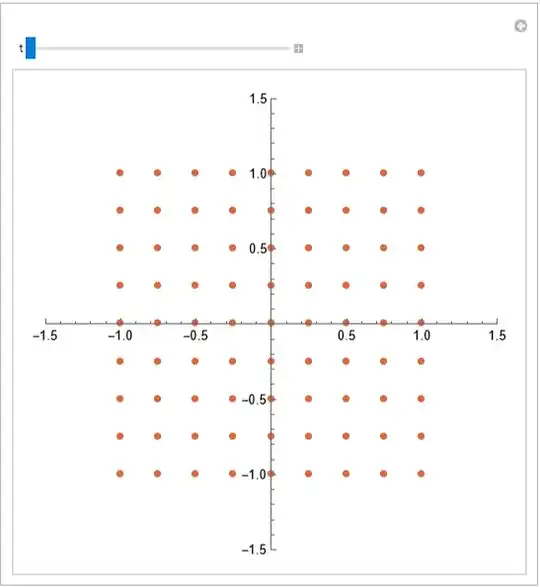
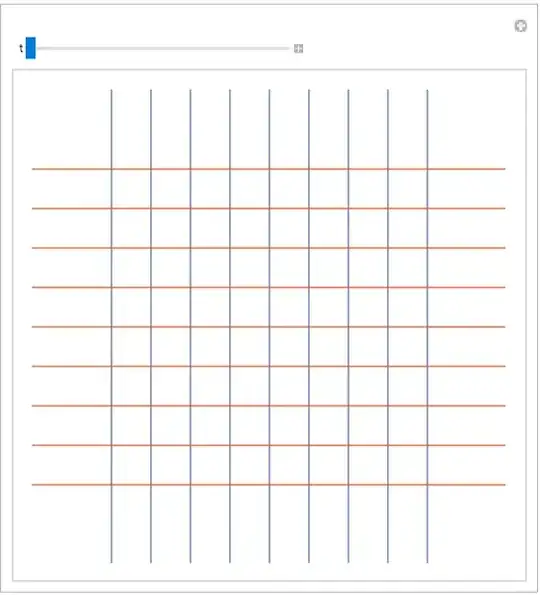
One can visualize linear transformation $P$ by animating action of $P^k$ for k between 0 and 1. Below is an attempt that does this with points. Ideally I would also like to visualize effect on the gridlines, what's an elegant way of doing this?

sqrtP = {{(2 Sqrt[29/3])/3, -(4/Sqrt[87])}, {0, 10/Sqrt[87]}};
animTrajectory[xs0_, A_] := Module[{},
   step = 0.025;
   xs = Table[
     Transpose[MatrixPower[A, k] . Transpose[xs0]], {k, 0, 1, step}];
   drawTrajectory[s_] := Graphics[{Opacity[.1], Point[xs[[;; s]]]}];
   drawTrajectories[s_] := 
    Graphics[{Opacity[.1]}~
      Join~(Line /@ Transpose[xs][[All, ;; s, All]])];
   combinedTrajectoryPlot[s_] := Show[
     ListPlot[xs0, PlotStyle -> Thick],
     ListPlot[xs[[s]], PlotStyle -> Red], drawTrajectories[s],
     PlotRange -> {{-1.3, 1.3}, {-1.3, 1.3}}, AspectRatio -> 1,
     GridLines -> Automatic,
     PlotLabel -> 
      StringForm[
       "coordinate transformation \!\(\*SuperscriptBox[\(``\), \
\(``\)]\)", MatrixForm[sqrtP], NumberForm[N[s*step], {3, 2}]]];
   plots = Table[combinedTrajectoryPlot[s], {s, 1, Length[xs]}];
   ListAnimate[plots]
   ];
gridPoints = Table[{x, y}, {x, -1, 1, .25}, {y, -1, 1, .25}];
gridPoints = Flatten[gridPoints, 1];
animTrajectory[gridPoints, sqrtP]

Should it looks like this, except you do P^k? https://youtu.be/PFDu9oVAE-g — Валерий Заподовников, Jul 12 '22 at 01:08
Somewhat related: https://mathematica.stackexchange.com/q/151238/1871 — xzczd, Jul 13 '22 at 14:28

score 4 · Accepted Answer · answered Jul 12 '22 at 05:46

sqrtP = {{(2 Sqrt[29/3])/3, -(4/Sqrt[87])}, {0, 10/Sqrt[87]}};
Animate[With[{matrix = MatrixPower[sqrtP, k]}, 
  ParametricPlot[{x, y} . matrix, {x, -2, 2}, {y, -2, 2}, 
   Mesh -> {10, 10}, MeshFunctions -> {#3 &, #4 &}, 
   MeshStyle -> {Blue, Red}, PlotRange -> 1.5, Axes -> False, 
   Frame -> False, 
   Epilog -> {Red, Arrow[{{0, 0}, {1, 0} . matrix}], Blue, 
     Arrow[{{0, 0}, {0, 1} . matrix}]}]], {k, 0, 1}, 
 ControlPlacement -> Top]

chyanog · Answer 2 · 2022-07-13T14:12:22.453

Manipulate[
  Module[{n = 9, range, pts0, pts1, sqrtP, mat},
  range = Range[-1., 1, 2/(n - 1)];
  pts0 = Tuples[range, 2];
  sqrtP = {{(2 Sqrt[29/3])/3, -(4/Sqrt[87])}, {0, 10/Sqrt[87]}};
  mat = MatrixPower[Transpose@sqrtP, k];
  pts1 = pts0.mat;
  Graphics[{
    Pink, Line@Transpose@{pts0, pts1},
    Gray, Line /@ Thread[{#, Reverse /@ #}.mat &@{{-2, #}, {2, #}} & /@ range],
    Riffle[{Blue, Red}, Translate[Disk[{0, 0}, 0.02], #] & /@ {pts0, pts1}]
    }, PlotRange -> 1.3]
  ], {k, 0, 1}]

score 3 · Answer 3 · answered Jul 12 '22 at 09:28

I've already pointed this out as an example of the utility of CoordinateBoundsArray[], so I'll present the following and direct you to that other discussion if you wish for more details:

mat = N[{{(2 Sqrt[29/3])/3, -(4/Sqrt[87])}, {0, 10/Sqrt[87]}}];
cba = Flatten[N[CoordinateBoundsArray[{{-1, 1}, {-1, 1}}, {Into[8], Into[8]}]], 1];
Manipulate[With[{tr = AffineTransform[MatrixPower[mat, t]][cba]}, 
                Graphics[{{AbsoluteThickness[0.4], Opacity[0.6], 
                           Line[Transpose[{cba, tr}]]},
                          {AbsolutePointSize[5],
                           {ColorData[97, 1], Point[cba]},
                           {ColorData[97, 4], Point[tr]}}},
                         Axes -> True, PlotRange -> 1.5]],
           {t, 0, 1}, SaveDefinitions -> True]

Manipulate of a linear transformation (1)

Since you also wanted to transform grid lines, here is another Manipulate[] that relies on Subdivide[] and InfiniteLine[] to do its job:

div = {N[Subdivide[-1, 1, 8]]};
divx = Transpose[PadRight[div, {2, Automatic}, 0.]];
divy = Reverse[divx, 2];
Manipulate[Block[{matp = MatrixPower[mat, t], tfun},
                 tfun = AffineTransform[matp];
                 Graphics[{{AbsoluteThickness[1],
                           {ColorData[97, 1],
                            InfiniteLine[#, matp[[All, 2]]] & /@ tfun[divx]},
                           {ColorData[97, 4],
                            InfiniteLine[#, matp[[All, 1]]] & /@ tfun[divy]}}},
                          PlotRange -> 1.5]],
           {t, 0, 1}, SaveDefinitions -> True]

Manipulate of a linear transformation (1)

I'll leave combining the grid line and point transformations into one Manipulate[] as an exercise.

I used AffineTransform[] in both Manipulate[] instances for readability purposes; if you wish to avoid the overhead of using transform functions for some reason, then we have the identity

AffineTransform[{{a, b}, {c, d}}][{{x1, y1}, ...}] ==
{{x1, y1}, ...} . Transpose[{{a, b}, {c, d}}]

Visualizing action of matrix

3 Answers3