1

I have a Matlab-style code that uses Fourier transform efficiently. Here is the function which defines a differentiation matrix D, where N denotes the modes number and kk is the wavenumber.

function [A,B,D,x]=func(N)
dxx=2*pi/N;x=dxx*((1:N)');
kk=[-N/2+1:N/2]';
C=diag(1i*kk);
A=exp(1i*x*kk');
B=exp(-1i*kk*x')/N;
D=A*(C*B);

In the main program, the differentiation matrix D can be used easily as an operator. For example, consider a function y(x). It uses a couple of lines to calculate the 1st- to 3rd-order derivatives.

N=64;
[A,B,D,x]=func(N);

D1=real(D);
D2=real(D^2);
D3=real(D^3);


Dy=D1y;
D2y=D2y;
D3y=D3*y;

I want to convert it exactly equivalently into Mathematica. I note that Mathematica provides the functions FourierTransform and FourierCoefficient, however, I found it has various parameter values for several different conventions, which is confusing. Can anyone please help to convert it as Mathematica code, and if you could give an example, it will be very helpful!

Update

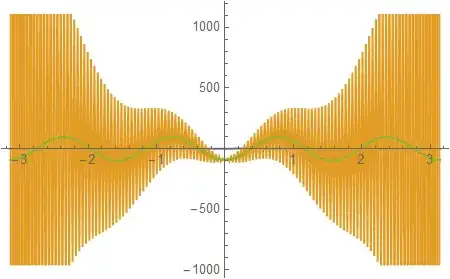
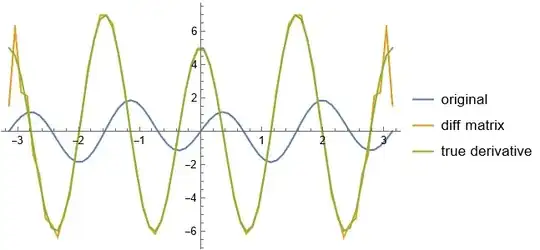
Thanks for the help of @J. M.'s persistent exhaustion and @user293787, I can calculate the 1st- and 2nd-order derivatives, but when using the code to calculate the 3rd-order derivative, the error is too large to be acceptable. I also tried use more modes with $n=256$, but the computational time became longer and the result became worse. Can you help to improve it? Thank you very much!

f3d[n_] := Module[{kk = Range[-n/2 + 1, n/2], x = 2*\[Pi]*Range[n]/n}, 
  Exp[I*KroneckerProduct[x, kk]].DiagonalMatrix[(I kk)^3].(Exp[-I*KroneckerProduct[kk, x]]/n)]

n = 128; (n = 256;)


(an exmaple)
f[x_] := Sin[x] Cos[3 x] + Sin[4 x];
vals = Table[N[f[x], 20], {x, -[Pi], [Pi], 2 [Pi]/(n - 1)}];
dddf = D[f[x], {x, 3}];
dddvals = Re[N[f3d[n], 20]].vals;
dddvalsTrue = Table[N[dddf, 20], {x, -[Pi], [Pi], 2 [Pi]/(n - 1)}];


thirdDplot = ListLinePlot[{vals, dddvals, dddvalsTrue}, DataRange -> {-[Pi], [Pi]}, PlotLegends -> {"original func", "diff matrix", "Exact derivative"}]

enter image description here

user95273
  • 135
  • 7
  • Concerning your Update: Your may have to take {x,-\[Pi],\[Pi]-2 \[Pi]/n,2 \[Pi]/n} in your tables, or something like that. But maybe this is getting out of hand here, I think @J.M. answered your original question. – user293787 Jul 23 '22 at 09:54
  • @user293787 did you mean the upper bounds of both two Table in my update should be modified. Could you explain a little? – user95273 Jul 23 '22 at 12:15
  • 1
    I changed two things, upper bound and stepsize. Why? In your Update-code the first x-value is $-\pi$ and the second is $+\pi$, which is the same point in a $2\pi$-periodic setting. Also, the stepsize must match the stepsize that you use in Exp[I*KroneckerProduct[x, kk]] which is $2\pi/n$. – user293787 Jul 23 '22 at 12:18
  • Why not NDSolve`FiniteDifferenceDerivative?: https://mathematica.stackexchange.com/q/182295/1871 – xzczd Jul 27 '22 at 05:32
  • Thank you for pointing out that link @xzczd, I have read that document for a whole day. According to my understand, when using Pseudospectral we should use a mesh with uniform nodes. However, in that link the author of that post used a non-uniform mesh. Could please write a short answer to show how to use your function func = NDSolveFiniteDifferenceDerivative[1, x, DifferenceOrder -> "Pseudospectral"]` to calculate the 3rd-order derivative of the example in the update of my post? Thank you again! – user95273 Jul 27 '22 at 14:32
  • grid = N@Range[-Pi, Pi, 2 Pi/25]; val = NDSolve`FiniteDifferenceDerivative[3, grid, f@grid, DifferenceOrder -> "Pseudospectral", PeriodicInterpolation -> True]; ListPlot[{grid, val}\[Transpose]]~Show~Plot[f'''[x], {x, -Pi, Pi}] "when using Pseudospectral we should use a mesh with uniform nodes" Yes, but only if PeriodicInterpolation -> True. Otherwise we need the Chebyshev-Gauss-Lobatto grid. Please read the document more carefully. – xzczd Jul 27 '22 at 14:45

1 Answers1

6

The code provided by the OP is actually pretty straightforward to translate:

fdm[n_] := Module[{kk = Range[-n/2 + 1, n/2], x = 2 π Range[n]/n},
    Exp[I KroneckerProduct[x, kk]] . DiagonalMatrix[I kk] .
    (Exp[-I KroneckerProduct[kk, x]]/n)]

where the matrix corresponding to D in the original MATLAB code is returned. (If you want to return the other stuff as well, I'll leave it as an exercise to figure out how to modify the function above.)

With that, here's a demo of how to use it as a differentiation matrix:

(* some periodic function *)
vals = Table[N[Sin[x] Cos[3 x] + Sin[4 x], 20], {x, -π, π, 2 π/(64 - 1)}];
(* estimated derivative from the differentiation matrix *)
dvals = Re[N[fdm[64], 20]] . vals;
(* true derivative for comparison *)
dvalsTrue = Table[N[-Cos[2 x] + 6 Cos[4 x], 20], {x, -π, π, 2 π/(64 - 1)}];

ListLinePlot[{vals, dvals, dvalsTrue}, DataRange -> {-π, π}, 
             PlotLegends -> {"original", "diff matrix", "true derivative"}]

a function and its derivatives

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
  • Hi, I use f2d[n_] :=Module[{kk = Range[-n/2 + 1, n/2], x = 2 \[Pi] Range[n]/n}, Exp[2*I KroneckerProduct[x, kk]].DiagonalMatrix[-kk^2].(Exp[-2* I KroneckerProduct[kk, x]]/n)] to produce the 2nd-derivation, which however gives incorrect result, please correct me, thank you! – user95273 Jul 23 '22 at 05:25
  • @user95273 Replace Exp[2*I...] by Exp[I...], and replace Exp[-2*I...] by Exp[-I...]. – user293787 Jul 23 '22 at 05:37
  • @user293787 thank you! it seems DiagonalMatrix[I kk] controls the derivative order. I tried DiagonalMatrix[(I kk)^3] for the 3rd-derivative, but the result looks incorrect. Could you explain a little more? – user95273 Jul 23 '22 at 07:21
  • @J. M.'s persistent exhaustion, by default, MATLAB uses 16 digits of precision, in order to obtain an exactly the same reuslt, does it mean I should use N[..., 16] for 16-digit precision? Thank you! – user95273 Jul 23 '22 at 07:29
  • 1
    @user95273 Take @J.M.'s code for one derivative, which uses a product of three matrices, and then only change the matrix in the middle, but do not change the first and last matrix. In the f2d code in your comment, you also changed the first and last matrix, by introducing extra factors of 2 compared to @J.M.'s code, but that is not what you want. Another possibility is f2dalternative[n_]:=MatrixPower[fdm[n],2]. – user293787 Jul 23 '22 at 07:30