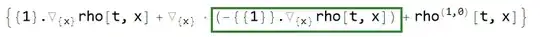How to set a adiabatic boundary conditions for a convection function?

Question

$\rho(x,t)$ is the probability function, $x\in[-1,1]$.

I'm trying to solve the convection function with adiabatic boundary condition as follows:

$$ \partial \rho/\partial t=D_t\frac{\partial^2\rho}{\partial x^2}-\frac{\partial (v_0\rho)}{\partial x} $$

On the boundary, $D_t\frac{\partial\rho}{\partial x}-v_0\rho=0$, which means current is zeros on the boundary.

The code is as the following:

<< NDSolve`FEM`
rWall=1;
v0[x_]:=1;
Subscript[D, t]=1
diffusePde=D[rho[x,t],t]+ D[rho[x,t] v0[x]-Subscript[D, t]D[rho[x,t],x],x]==
             NeumannValue[0,True];
ic=rho[x,0]==1/(2 Pi σ^2)Exp[-(x^2)/(2  σ^2)]/.σ->0.1;
lineMesh=ToElementMesh["Coordinates"->Partition[Range[-rWall,rWall,1/1000],1],
           "MeshElements"->{LineElement[Table[{x,x+1},{x,1,1000}]]}];
usol=NDSolveValue[{diffusePde,ic},rho,{x,-rWall,rWall},{t,0,100}];
gflist=Table[Plot[usol[x,t],{x,-rWall,rWall},PlotRange->All],{t,0,1,0.1}];
ListAnimate[gflist]

But the integral doesn't conserve. Is there anything wrong with may code? Thanks for your help.

Please show us the complete code sample. – xzczd Jul 27 '22 at 09:39 — xzczd, Jul 27 '22 at 09:39
thanks for your help, I've edited the question. – 江蛮子 Jul 28 '22 at 01:15 — 江蛮子, Jul 28 '22 at 01:15

xzczd · Accepted Answer · 2022-08-15T11:47:26.700

Another problem related to NeumannValue and formal form of PDE. As discussed in e.g. this post, to properly set the NeumannValue, we need to check the underlying formal form:

NDSolve`FEM`GetInactivePDE@
 First@NDSolve`ProcessEquations[{diffusePde, ic}, rho, {x, -rWall, rWall}, {t, 0, 100}]

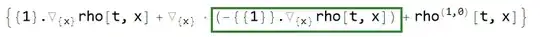
So NDSolve internally doesn't transform the PDE to the form in your mind. You're expecting something like

$$\frac{\partial \rho}{\partial t}=\frac{\partial}{\partial x}\left(D_t\frac{\partial\rho}{\partial x}-v_0\rho\right)$$

right? This form is also allowed by FiniteElement method, but we need to help it a bit with Inactive (Related examples can be found in tutorial NeumannValue and Formal Partial Differential Equations):

With[{rho = rho[x, t]}, 
 diffusePdeInactive = 
   D[rho, t] == 
    Inactive[Div][
     Subscript[D, t] Inactive[Grad][rho, {x}] - Inactive[Times][{v0[x]}, rho], {x}];]

I've omitted NeummanValue in the code, because Neumann 0 condition is the default setting of FiniteElement method.

Let's again check the underlying formal PDE:

NDSolve`FEM`GetInactivePDE@
 First@NDSolve`ProcessEquations[{diffusePdeInactive, ic}, 
   rho, {x, -rWall, rWall}, {t, 0, 100}]

As we can see, the $v_0 \rho$ term is in the desired position. Alternatively we can check the $\alpha$ term with:

state = First@
   NDSolve`ProcessEquations[{diffusePdeInactive, ic}, 
    rho, {x, -rWall, rWall}, {t, 0, 100}];
data = state["FiniteElementData"]["PDECoefficientData"];
data["ConservativeConvectionCoefficients"]
(* {{{{1}}}} *)

In contrast:

state = First@
   NDSolve`ProcessEquations[{diffusePdeInactive, ic} // Activate, 
    rho, {x, -rWall, rWall}, {t, 0, 100}, 
    Method -> {"MethodOfLines", "SpatialDiscretization" -> "FiniteElement"}];
data = state["FiniteElementData"]["PDECoefficientData"];
data["ConservativeConvectionCoefficients"]
(* {{{{0}}}} *)

Now the integral conserves:

usol2 = 
  NDSolveValue[{diffusePdeInactive, ic}, rho, {x, -rWall, rWall}, {t, 0, 100}];
Table[NIntegrate[usol2[x, t], {x, -rWall, rWall}], {t, 0, 1, 0.1}]
(*
{3.98942, 3.98942, 3.98942, 3.98944, 3.98943, 
 3.98943, 3.98943, 3.98943, 3.98943, 3.98943, 3.98943}
 *)

Alternatively, we can live with the default formal PDE. In this case we need to adjust the NeumannValue to

With[{rho = rho[x, t]}, 
  diffusePde3 = 
   D[rho, t] + D[rho v0[x] - Subscript[D, t] D[rho, x], x] == 
    NeumannValue[v0[x] rho, x == rWall] + NeumannValue[-v0[x] rho, x == -rWall]];
usol3 = 
  NDSolveValue[{diffusePde3, ic}, rho, {x, -rWall, rWall}, {t, 0, 100}];
Table[NIntegrate[usol3[x, t], {x, -rWall, rWall}], {t, 0, 1, 0.1}]
(* {3.98942, 3.98942, 3.98942, 3.98944, 3.98943, 3.98943, 3.98943, 3.98943,
3.98943, 3.98943, 3.98943} *)

But since setting the NeumannValue is so troublesome, why not the good old TensorProductGrid?:

With[{rho = rho[x, t]}, 
 pdeold = D[rho, t] + D[rho v0[x] - Subscript[D, t] D[rho, x], x] == 0;
 bc = rho v0[x] - Subscript[D, t] D[rho, x] == 0 /. {{x -> -rWall}, {x -> rWall}};]
usolold = 
  NDSolveValue[{pdeold, ic, bc}, rho, {x, -rWall, rWall}, {t, 0, 100}];
Table[NIntegrate[usolold[x, t], {x, -rWall, rWall}], {t, 0, 1, 0.1}]
(* {3.98942, 3.98942, 3.98942, 3.98942, 3.98942, 
    3.98942, 3.98942, 3.98942, 3.98942, 3.98942, 3.98942} *)

Thanks! I have one more question. When $t>\infty$, I get a stable usol. But if I change the Pde to poison Pde, the result usol is a flat line. ``` With[{rho = rho[x]}, poissonPde = D[rho v0[x] - Subscript[D, t] D[rho, x], x] == NeumannValue[Sign[x] v0[x] rho, Abs[x] == rWall];] usolPoisson = NDSolveValue[{poissonPde}, rho, {x, -rWall, rWall}];```` How shall I modify it? — 江蛮子, Jul 29 '22 at 02:44
@江蛮子 That's expected, notice in this case there exist infinite many solutions, and rho[x]==0 is definitely one of them. — xzczd, Jul 29 '22 at 03:08
Thanks! Mathematica tutrial says we can use NDsolve to get all solutions, but NDsolve doesn't work for my question. How shall I set integral conditions or anything else to get the non trivial solution? — 江蛮子, Jul 29 '22 at 06:37
@江蛮子 “Mathematica tutrial says we can use NDsolve to get all solutions” What do you mean by "all solutions"? Which part of the tutorial are you refering to? NDSolve is definitely not designed for general solutions. Actually if you don't call FiniteElement, there will be a warning suggesting the current b.c.s are not sufficient to determine particular solution(s): rWall = 1; With[{rho = rho[x]}, pdeold = D[rho, t] + D[rho - D[rho, x], x] == 0; bc = rho - D[rho, x] == 0 /. {{x -> -rWall}, {x -> rWall}}]; NDSolve[{pdeold, bc}, rho, {x, -rWall, rWall}]. — xzczd, Jul 29 '22 at 06:52
@江蛮子 "How shall I set integral conditions or anything else to get the non trivial solution?" This is a totally different problem, please ask a new question rather than discussing in comment. — xzczd, Jul 29 '22 at 06:53
In the document of NDsolveValue-existing problem-multiple solution. (I'm reading the Chinese version, the translation may be wrong). It gives an example of using NDsolve to find all solutions. But it may only be useful in some examples. — 江蛮子, Jul 29 '22 at 07:19
@江蛮子 You misunderstand the document, it means that, when there exist multiple particular solutions, NDSolveValue will return only one of them, but NDSolve will return all the solutions found by the solver. (See also https://mathematica.stackexchange.com/a/186582/1871) Your problem is different, the underlying issue is you haven't set enough b.c.s. This is mentioned in Details section of NDSolve: "The differential equations must contain enough initial or boundary conditions to determine the solutions for the $u_i$ completely."(微分方程必须包括足够的初始条件或边界条件来完全确定 $u_i$ 的解.) — xzczd, Jul 29 '22 at 07:33
@江蛮子 It's also mentioned in tutorial Numerical Solution of Differential Equations. Read the paragraph started with "When you use NDSolve, the initial or boundary conditions you give must be sufficient to determine the solutions for the $y_i$ completely. ..." (使用 NDSolve 时，给定的初始或者边界条件必须能完全确定 $y_i$ 的解. …) — xzczd, Jul 29 '22 at 07:37

How to set a adiabatic boundary conditions for a convection function?

1 Answers1

Linked