0

how I can use StreamPlot or VectorPlot to show x[t] and 1-x[t] and show convergence point in my plot with a different colour like a blue point?

G1 = 21290/27
G2 = 23879130/2809
G3 = 13572050/2809
G4 = 1809025/288

U1[t_] := x[t] (G1) + (1 - x[t]) (G2)
U2[t_] := (1 - x[t]) (G3) + x[t] (G4)


x'[t] == x[t] (1 - x[t]) (U1[t] - U2[t])

I want to plot something like below pic:

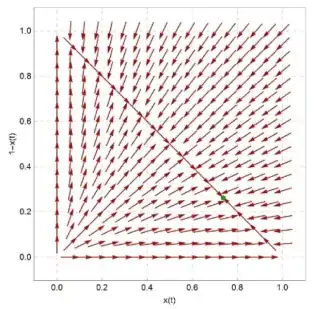
enter image description here

Ahmad
  • 77
  • 5
  • Use the option Epilog -> {Blue, Point[{...,...}]} in StreamPlot, where ... should be replaced by appropriate coordinates. – Michael E2 Jul 29 '22 at 17:18
  • Some examples: q/64407, a/80285, a/203247, a/223202, a/242409 – Michael E2 Jul 29 '22 at 17:27
  • Is the plot that you are showing above the one that you want to reproduce? – demm Jul 29 '22 at 21:07
  • @demm, yes, I want to plot like that with x[t] and 1-x[t] that I mentioned in my question. – Ahmad Jul 29 '22 at 21:20
  • @Michael E2, Thanks, my first question is how to plot x[t] and 1-x[t] like above pic. – Ahmad Jul 29 '22 at 21:25
  • The plot doesn't make sense to me and seems to have an undefined relationship to your diff. eqn. If the axis labels indicate coordinates, how can you can there be a point at x[t] == 0.4 and 1 - x[t] == 0.2, say? The conditions are inconsistent. As coordinates {x[t], 1 - x[t]} parametrizes the diagonal. The vector field below/above looks like ±{x,1-y} in {x,y}-coordinates with special cases along the diagonal. You should probably specify the components of the vector field, mathematically if not in code. – Michael E2 Jul 29 '22 at 22:43
  • This shows a similar vector field with an arbitrarily chosen point of convergence: With[{am = ArrayMesh[SparseArray[{{_, _} -> 1}, {15, 15}, 0]]}, mesh = MeshRegion[ Rescale@MeshCoordinates[am], MeshCells[am, 2] ] ]; VectorPlot[Piecewise[{ {{x, y}, x < 1 - y}, {-{x, y}, x > 1 - y}, {{1, -1}, x == 1 - y && x < 7/10}}, {-1, 1}], {x, y} \[Element] mesh, FrameLabel -> {x, y}, VectorPoints -> "Mesh", Epilog -> {Blue, PointSize@Medium, Point[{7/10, 1 - 7/10}]}] – Michael E2 Jul 29 '22 at 23:11
  • @Michael E2, I apperetiate you for your help. Like you, I am confused as to how such a thing is possible. I see this plot in a paper at: (https://www.sciencedirect.com/science/article/abs/pii/S0306261922004706) you can see this plot at page 9 and related eq at page 6 of this paper. – Ahmad Jul 29 '22 at 23:23

0 Answers0