I have this simple Do Loop that, for some reason, takes a really long time for $h<\frac{1}{15}$. Why is this so? Is there a more efficient way in programming such a recursion?
h = 1/20;
v1[0] = 1;
v2[0] = 0;
Do[v1[j + h] = h v2[j] + v1[j];
v2[j + h] = h (v2[j] + 1/v1[j]) + v2[j], {j, 0, 2, h}]
As @Domen says, use machine-precision numbers instead of exact rationals. Apart from this, I'd comment that there is no need to pre-compute the numbers in a Do loop: it is more Mathematica-style to define a memoizing recursion and then access the functions $v_1(j)$ and $v_2(j)$ randomly (without having to be explicit about the order of their evaluation):
h = 1/20;
Clear[v1, v2];
v1[0] = 1.;
v2[0] = 0.;
v1[j_ /; Divisible[j, h] && j > 0] := v1[j] = h v2[j - h] + v1[j - h];
v2[j_ /; Divisible[j, h] && j > 0] := v2[j] = h (v2[j - h] + 1/v1[j - h]) + v2[j - h];
ListPlot[Transpose@Table[{{j, v1[j]}, {j, v2[j]}}, {j, 0, 2, h}], PlotLegends -> {"v1", "v2"}]
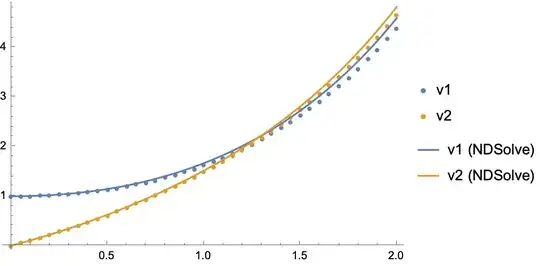
The NDSolve curves in the above plot give the limit $h\to0^+$ and were calculated with
NDSolve[{v1''[j] == v1'[j] + 1/v1[j], v1[0] == 1, v1'[0] == 0}, v1, {j, 0, 2}]
Random access without explicit in-order precomputation:
v1[3]
(* 12.2335 *)
v2[7]
(* 629.188 *)
v1[0] = 1; v2[0] = 0;withv1[0] = 1.; v2[0] = 0.;– Domen Aug 04 '22 at 12:37h = 1/15, yourv2[2]is a rational number where numerator and denominator have millions of digits. – user293787 Aug 04 '22 at 12:41NDSolve[{v1'[j] == v2[j], v2'[j] == v2[j] + 1/v1[j], v1[0] == 1, v2[0] == 0}, {v1, v2}, {j, 0, 2}]or even justNDSolve[{v1''[j] == v1'[j] + 1/v1[j], v1[0] == 1, v1'[0] == 0}, v1, {j, 0, 2}]– Roman Aug 04 '22 at 13:17