Interpolating and plotting a surface for a sparse set of 3d data points

Question

I have a set of $(x,y,z)$ coordinates which sparsely cover a surface, e.g.:

data = {{51, 15, 0.1}, {300, 11, 0.99}, {140, 22, 0.123}, {54, 12, 0.66}, ...};

What is a good general method, in Mathematica 9, of interpolating and plotting a surface for this sparse data set? Graphics3D[BSplineSurface[data]] doesn't seem to get the job done; the output is a planar rectangle.

Interpolation works for multidimensional functions but You have to be sure that there are no duplicates in {x,y} with different z. Interpolation[{{#1, #2}, #3} & @@@ data] — Kuba, Jun 18 '13 at 06:07
@m_goldberg ListPlot3D seems to do what I'd like, so thanks! But do you know what interpolation method is being used? — InsM, Jun 18 '13 at 06:29

Stefan · Answer 1 · 2013-06-18T07:01:12.617

I'd go with ListPointPlot3D.

ListPoint3D generates a 3D scattered plot of points with coordinates {xi,yi,zi}.

Since you're a bit avaricious with your data, here the plot with your data:

data = {{51, 15, 0.1}, {300, 11, 0.99}, {140, 22, 0.123}, {54, 12, 0.66}};
ListPointPlot3D[data, PlotStyle -> PointSize[0.03], Filling -> Bottom,
   ViewPoint -> {0, 0, \[Infinity]}]

enter image description here

Edit:

If you want to use BSpline, just take a BSplineCurve, if your data does not produce a decent surface:

Graphics3D[{BSplineCurve[data], PointSize[Medium], Green, Line[data], 
    Red, Point[data]}, BoxRatios -> {2, 2, 2}]

enter image description here

Edit2:

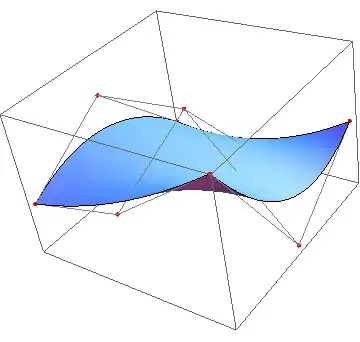
For a BSplineSurface (with qualified data) you can do something like:

data=Table[{i, j, RandomReal[{-1, 1}]}, {i, 3}, {j, 3}];
Show[Graphics3D[{PointSize[Medium], Red, Map[Point, data], Gray, 
    Line[data], Line[Transpose[data]]}], Graphics3D[BSplineSurface[data]]]

enter image description here

Thanks, but I'm specifically looking for a surface! – InsM Jun 18 '13 at 06:33 — InsM, Jun 18 '13 at 06:33
so why not pasting your data completely? – Stefan Jun 18 '13 at 06:49 — Stefan, Jun 18 '13 at 06:49

score 1 · Accepted Answer · answered Jun 18 '13 at 06:53

1

You can use the option InterpolationOrder to control the degree of smoothing.

SeedRandom[42]; data = RandomReal[10, {20, 3}];
Column[
 ListPlot3D[data,
    ImageSize -> Medium,
    Mesh -> None,
    InterpolationOrder -> #] & /@ Range[0, 2]]

enter image description here

answered Jun 18 '13 at 06:53

m_goldberg

107,779
16
103
257

Setting InterpolationOrder greater than 1 doesn't seem to make a difference unless you have regular data (sampled on a grid)... – Jun 18 '13 at 07:37

Interpolating and plotting a surface for a sparse set of 3d data points

2 Answers2