0

I am very new to Mathematica set up and I have the following question: I have a bivariate probability distribution which is a little complicated and of the form:

$$f(x,y)=(a_0+a_1+a_2)\frac{a_1 a_2}{a_0}\exp(-a_1 x-a_2 y)\left\{1-\exp\left[-a_0\min(x,y)\right]\right\}$$

such that, $x>0$ and $y>0$.

I need to simulate from the above distribution.

Any suggestion is highly appreciated.

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
Indranil
  • 1
  • 1

1 Answers1

2

If I understood it correctly, you can try this:

pdf[x_, y_] := (a0 + a1 + a2)*((a1*a2)/a0)*Exp[-a1 x - a2 y]*(1 - Exp[-a0 Min[x, y]])

and then, assigning the value of 1 to a0, a1 and a2, you can plot it:

Plot3D[Evaluate@pdf[x, y] /. {a0 -> 1, a1 -> 1, a2 -> 1}, 
  {x, 0, 4}, {y, 0, 6}, ColorFunction -> "Rainbow", 
  PlotRange -> All, Mesh -> Full, Exclusions -> None]

Result:

enter image description here

EDITED

If you want to "simulate" from the continuous probability distribution, you might want to use Manipulate[] to see what happens when you change parameters a0, a1 and a2:

Manipulate[
  Plot3D[Evaluate@pdf[x, y] /. {a0 -> v0, a1 -> v1, a2 -> v2}, {x, 0, 4}, {y, 0, 4},   
  ColorFunction -> "Rainbow", PlotRange -> All, 
  Mesh -> Full, Exclusions -> None],
  {{v0, 1, "a0"}, .001, 1, .001},
  {{v1, 1, "a1"}, .001, 1, .001},
  {{v2, 1, "a2"}, .001, 1, .001}]

Result:

enter image description here

EDITED

The discrete case:

DiscretePlot3D[Evaluate@pdf[x, y] /. {a0 -> 1, a1 -> 1, a2 -> 1}, 
  {x, 0, 4, .1}, {y, 0, 4, .1}, ColorFunction -> "Rainbow", PlotRange -> All]

Result:

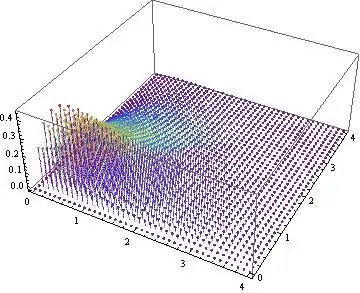
enter image description here

EDITED

You could also plot the ContourPlot[] of your distribution:

ContourPlot[pdf[x, y] /. {a0 -> 1, a1 -> 1, a2 -> 1}, 
  {x, 0, 4}, {y, 0, 4}, ColorFunction -> "Rainbow", 
  PlotRange -> All, Exclusions -> None]

Result:

enter image description here

Rod
  • 3,318
  • 2
  • 24
  • 40
  • I think that the OP means that he/she wants to sample from the given distribution, that is draw a series of independent random variables that follow the given probability law. – Aditya Jun 19 '13 at 03:37
  • Thanks folks for the response.I already knew these things but what I am having trouble is to get bivariate random samples (x1,y1),...(xn,yn) from the above distribution for a random sample of size n. – Indranil Jun 19 '13 at 23:30