6

This question derives directly from this one, but concerns instead a different matter... one related to display format.

This integral

$$I = \int\limits_2^4 \frac{\sqrt{\log (9-x)}}{\sqrt{\log (9-x)}+\sqrt{\log (x+3)}} \, dx$$

cannot be solved directly by Mathematica:

Integrate[
     Sqrt[Log[9 - x]]/(Sqrt[Log[9 - x]] + Sqrt[Log[x + 3]]), 
     {x, 2, 4}]

As shown in the linked problem, if you give Mathematica a substitution hint (based on the symmetry of the terms in the integrand), then it can solve the integral:

Integrate[
    Sqrt[Log[9 - x]]/(Sqrt[Log[9 - x]] + Sqrt[Log[x + 3]]) /. 
    {x -> y + 3}, 
    {y, -1, 1}]

(* 1 *)

I strongly prefer to display my input in mathematical typography (with integral signs and such),

enter image description here

How does one assert the change in variables (above) in the mathematical typography that shows integral signs and such? I could go in by hand and replace the limits on the integral, the arguments in the integrand, and so on, but that seems very awkward indeed.

I've tried the rather obvious tricks based on Assuming and Replace and so on, but none work, for example

Integral with replace rule

Of course this particular integral is just an example. I'd like a general approach.

David G. Stork
  • 41,180
  • 3
  • 34
  • 96
  • 1
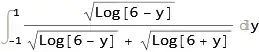
    Probably the following: int1 = Inactive[Integrate][Sqrt[Log[9 - x]]/(Sqrt[Log[9 - x]] + Sqrt[Log[x + 3]]), {x, 2, 4}]; int2 = ReplacePart[MapAt[ReplaceAll[#, x -> y + 3] &, int1, {1}], 2 -> {y, -1, 1}]; int2//Activate is not what you are looking for. Am I right? – Alexei Boulbitch Aug 14 '22 at 06:19
  • Although helpful, you're right: that's not what I'm seeking. I must SEE the integral sign. Motivation: I make Mathematica presentations in front of my class, and I want the students to see mathematical typography to better think as mathematicians rather than code and computer scientists. – David G. Stork Aug 14 '22 at 15:38

2 Answers2

8

You could use the new in V 13.1 IntegrateChangeVariables

int = Inactive[Integrate][Sqrt[Log[9 - x]]/(Sqrt[Log[9 - x]] + Sqrt[Log[x + 3]]), {x, 2, 4}]

Mathematica graphics

IntegrateChangeVariables[int, y, y == x - 3]

Mathematica graphics

Activate[%]

Mathematica graphics

How does one assert the change in variables (above) in the mathematical typography

I do not know if the above does what you want, as the change of variable is done internally.

But if you want to display the step in Latex, then you could do

TeXForm[HoldForm[
  IntegrateChangeVariables[
   Inactive[Integrate][
    Sqrt[Log[9 - x]]/(Sqrt[Log[9 - x]] + Sqrt[Log[x + 3]]), {x, 2, 
     4}], y, y == x - 3]]]

Which compiles to

enter image description here

I would manually edit the Latex and remove IntegrateChangeVariables in final version (if you do not want it) which gives

enter image description here

Nasser
  • 143,286
  • 11
  • 154
  • 359
  • Thanks so much. I should have mentioned that I run v. 11.3, but this IntegrateChangeVariables looks so useful that I guess I'll upgrade. I'm not interested in $\LaTeX$ here (but thanks anyway!), rather Mathematica typography where the integral sign is visible (rather than Integrate[...]. I like to show math symbols in my class lectures to help my students think about math rather than coding. The short answer (thanks): Yes... this is all solved in v. 13... so I must upgrade. ($\checkmark$) – David G. Stork Aug 14 '22 at 15:44
5

Since your concern is primarily with display, an approach focused on display using IntegrateChangeVariables recommended by Nasser:

$Version

"13.1.0 for Mac OS X x86 (64-bit) (June 16, 2022)"


Clear["Global`*"]


Column[{"Expression to be integrated",
   eqn1 =
    f[x] == Sqrt[Log[9 - x]]/(Sqrt[Log[9 - x]] + Sqrt[Log[x + 3]]),
   "\nIntegrating",
   eqn2 = ApplySides[Inactive[Integrate][#, {x, 2, 4}] &, eqn1],
   "\nChange of variables",
   ConditionalExpression[(eqn3 = 
        ReplacePart[
         eqn2, -1 -> IntegrateChangeVariables[eqn2[[-1]], y, #]]), #] &[
    y == x - 3],
   "\nEvaluating",
   eqn4 = ReplacePart[eqn3, -1 -> Activate[eqn3[[-1]]]],
   "\nResult",
   eqn5 = ReplacePart[eqn4, {1, 1} -> eqn1[[-1]]]}] //
 TraditionalForm

enter image description here

Bob Hanlon
  • 157,611
  • 7
  • 77
  • 198
  • Nice typography... above and beyond the call of duty! ($+1$). The core needed functionality was covered by Nasser, however. – David G. Stork Aug 14 '22 at 19:44