3

I am numerically solving the following ODE below. If I set AccuracyGoal and PrecisionGoal both to 10 I get a solution that makes sense: constant and then damped oscillation. However, all things equal, if I increase the Accuracy and Precision goals at some point the solution stops making sense. Why?

ti = 2 10^12;
tf = 2 10^14;
m=1;

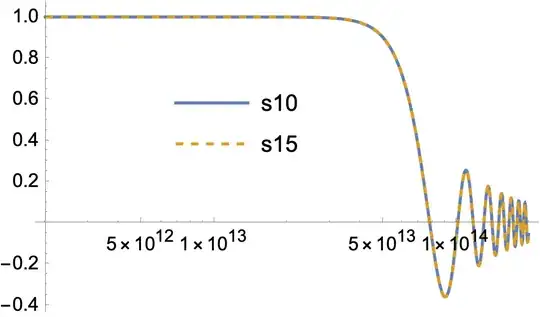
s10 = NDSolve[{a''[t] + 3/(2 t) a'[t] + m^2 (8 10^-21 t)^4 a[t] == 0, a[ti] == 1, a'[ti] == 0}, a[t], {t, ti, tf}, AccuracyGoal -> 10, PrecisionGoal -> 10];
s15 = NDSolve[{a''[t] + 3/(2 t) a'[t] + m^2 (8 10^-21 t)^4 a[t] == 0, a[ti] == 1, a'[ti] == 0}, a[t], {t, ti, tf}, AccuracyGoal -> 15, PrecisionGoal -> 15];


LogLinearPlot[{a[t] /. s10, a[t] /. s15}, {t, ti , tf}, PlotRange -> All]

enter image description here

Rudyard
  • 471
  • 2
  • 7

1 Answers1

10
Clear["Global`*"]

ti = 2 10^12;
tf = 2 10^14;

m = 1/4;

eqns = {a''[t] + 3/(2 t) a'[t] +
     m^2 (8 10^-21 t)^4 a[t] == 0,
   a[ti] == 1, a'[ti] == 0};

From the documentation for PrecisionGoal, "In most cases, you must set WorkingPrecision to be at least as large as PrecisionGoal."

s10 = NDSolve[eqns, a[t], {t, ti, tf},
   WorkingPrecision -> 12,
   AccuracyGoal -> 10,
   PrecisionGoal -> 10];

s15 = NDSolve[eqns, a[t], {t, ti, tf},
   WorkingPrecision -> 17,
   AccuracyGoal -> 15,
   PrecisionGoal -> 15];


LogLinearPlot[{a[t] /. s10, a[t] /. s15}, {t, ti, tf}, 
 PlotRange -> All,
 PlotStyle -> {Automatic, Dashed},
 PlotLegends -> Placed[{"s10", "s15"}, {.4, .6}]]

enter image description here

Bob Hanlon
  • 157,611
  • 7
  • 77
  • 198
  • Thanks. If I set m=1 instead of your 1/4. The solution blows up as it is. If I decrease precision, for example to WorkingPrecision -> 15, AccuracyGoal -> 10, PrecisionGoal -> 10 it behaves properly again. So now, for different reasons, it looks like the solution gets worse I as we increase precision... – Rudyard Aug 23 '22 at 12:57
  • As the value of m approaches 1 the WorkingPrecision in NDSolve must be increased even more above the specified PrecisionGoal and you must also specify a WorkingPrecision in the LogLinearPlot – Bob Hanlon Aug 23 '22 at 13:48