Flux boundary condition on a line using derivatives

Question

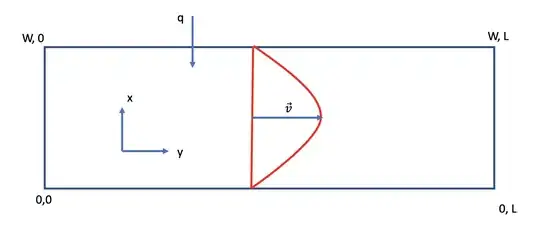
I am solving a partial differential equation for heat-transport on a rectangular domain of width W and length L with fluid flow.

$$ v_{max}\bigg(1-\bigg(\frac{x-W/2}{W/2}\bigg)^2\bigg) \frac{\partial T(x,y)}{\partial y} = \alpha \bigg[\frac{\partial^2}{\partial x^2}T(x,y)+\frac{\partial^2}{\partial y^2}T(x,y)\bigg]+Q$$.

The code for the equation is here:

Subscript[v, max] (1 - ((x - W/2)/(W/2))^2) Inactive[Grad][T[x, y], y] == \[Alpha] (Inactive[Laplacian][T[x, y], x] + Inactive[Laplacian][T[x, y], y]) + Q

I want to impose a flux condition on one of the walls without using a NeumannValue function. Basically I want the following the following boundary condition:

$ -k\frac{\partial T}{\partial x} = q$ when ${x,y} \in Line[\{W,0\},\{W,L\}]$

I do not want to use the following piece of code so as to avoid the complications with the definition of NeumannValue with velocities.

NeumannValue[q, {x, y} \[Element] Line[{{W, 0}, {W, L}}]]

My question is whether I can write the boundary condition on the left-hand side without NeumannValue. Can I write the flux BC on a line using Derivative or D?

I understand it can be done for one variable (e.g. D[T[x],x]/.x->0 == q). How to do this for a line, where $(x,y) \in Line[\{W,0\},\{W,L\}]$?