Let consider the local discontinuous Galerkin method in application to solve system of ODEs. The theory is discussed here. The implementation is very straightforward. In this example we use Euler polynomials and Gauss formula for integration
params = {a -> 0.4, m -> 2.4, Izz -> 1.0, g -> 9.81, fc -> 13.6829};
T = 2.0; kmax = 30;
Get["NumericalDifferentialEquationAnalysis`"];
UT[mm_, t_] := EulerE[mm, t];
M0 = 5; nn = 12; ns = 4; np = 5; tmax = 2;
y[t_] = Table[Symbol["y" <> ToString[i]][t], {i, 1, ns}];
eqs = {q'[t] == z[t],
z'[t] == (-a g m Sin[q[t]] - fc Tanh[k z[t]] + x[t])/(Izz + a^2 m),
p'[t] == (a g m Cos[q[t]] x[t])/(Izz + a^2 m),
x'[t] == -p[t] + (fc k Sech[k z[t]]^2 x[t])/(Izz + a^2 m)}; F =
Table[eqs[[i, 2]], {i, ns}]; var = {q[t], z[t], p[t],
x[t]}; ini = {0, 0, pb, xb}; bc2 = {8/10, 0}; ff =
Table[F /. Table[var[[i]] -> y[t][[i]], {i, ns}] /.
params /. {k -> (7 + kap)/10}, {kap, 0, kmax}];
LDGODEs[M0_, nn_, ns_, np_, f_, ini_, tmax_, kap_] :=
Module[{dx = tmax/nn, A = Array[aa, {M0 + 1, nn, ns}]},
xl = Table[ l*dx, {l, 0, nn}];
psi[mm_, k_, t_] :=
Piecewise[{{UT[
mm, (2 t - xl[[k + 1]] - xl[[k]])/(xl[[k + 1]] - xl[[k]])],
xl[[k]] <= t <= xl[[k + 1]]}, {0, True}}];
gg = Table[
GaussianQuadratureWeights[np, xl[[i]], xl[[i + 1]]], {i, nn}];
dp = Table[
D[UT[mm, (2 t - xl[[k + 1]] - xl[[k]])/(xl[[k + 1]] - xl[[k]])],
t], {k, nn}];
rul = Table[
y[t][[i]] ->
Sum[aa[mm, k, i] psi[mm - 1, k, t], {mm, 1, M0 + 1}, {k, 1,
nn}], {i, ns}];
eq = Flatten[
Table[-Sum[
aa[i + 1, n,
ks] (Table[(psi[i, n, t] If[j == 0, 0,
dp[[n]] /. mm -> j]), {t, gg[[n]][[All, 1]]}] .
gg[[n]][[All, 2]]), {i, 0,
M0}] - (Table[(f[[ks]] /. rul) psi[j, n, t], {t,
gg[[n]][[All, 1]]}] . gg[[n]][[All, 2]]), {j, 0, M0}, {n,
1, nn}, {ks, ns}] +
Table[Sum[
aa[i + 1, n,
ks] (psi[i, n, xl[[n + 1]]] psi[j, n, xl[[n + 1]]]), {i, 0,
M0}] - Sum[
If[n < 2, ini[[ks]]/(M0 + 1),
aa[i + 1, n - 1, ks] psi[i, n - 1, xl[[n]]]] psi[j, n,
xl[[n]]], {i, 0, M0}], {j, 0, M0}, {n, 1, nn}, {ks, ns}]];
bc = Table[
Sum[aa[i + 1, k, s] psi[i, k, 2], {i, 0, M0}, {k, nn}] ==
bc2[[s]], {s, 1, 2}];
eqn = Table[eq[[k]] == 0, {k, Length[eq]}];
var = Join[Flatten[A], {pb, xb}];
soln = FindRoot[Join[eqn, bc],
Table[{var[[i]], If[kap == 0, 1/10, var[[i]] /. soln]}, {i,
Length[var]}]];
soln];
Solution
Do[
ldgsol[kap] =
LDGODEs[M0, nn, ns, np, ff[[kap + 1]], ini, tmax, kap];, {kap, 0,
kmax}] // AbsoluteTiming
In the end we have one message from FindRoot
FindRoot::lstol: The line search decreased the step size to within tolerance specified by AccuracyGoal and PrecisionGoal but was unable to find a sufficient decrease in the merit function. You may need more than MachinePrecision digits of working precision to meet these tolerances.
It means that step with k=3.7 is a limit of this code with current parameters. Visualization
leg = {"q", "z", "p", "x"};
Table[Plot[
Evaluate[
Table[Sum[aa[i + 1, k, s] psi[i, k, t], {i, 0, M0}, {k, nn}] /.
ldgsol[kap], {kap, 0, kmax, 1}]], {t, 0, tmax}, PlotRange -> All,
PlotLegends -> Table[(7. + n)/10, {n, 0, kmax, 1}], Frame -> True,
PlotLabel -> leg[[s]]], {s, ns}]
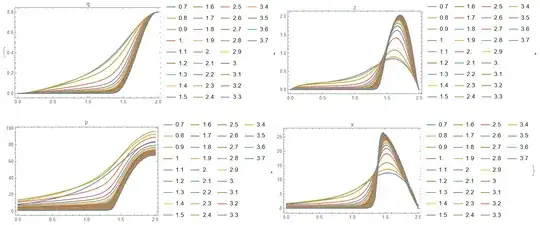
Using this solution we can generate initial data for NDSolve and generate new solution
data = Table[{.7 + kk/10, pb, xb} /. ldgsol[kk], {kk, 0, kmax, 1}];
sol1 = Table[
NDSolveValue[{q'[t] == z[t],
z'[t] == (-a g m Sin[q[t]] - fc Tanh[k z[t]] + x[t])/(Izz +
a^2 m), p'[t] == (a g m Cos[q[t]] x[t])/(Izz + a^2 m),
x'[t] == -p[t] + (fc k Sech[k z[t]]^2 x[t])/(Izz + a^2 m),
q[0] == 0, z[0] == 0, p[0] == data[[i, 2]],
x[0] == data[[i, 3]]} /. params /. k -> data[[i, 1]], {q, z, p,
x}, {t, 0, T}], {i, Length[data]}];
Finally we compare LDG numerical solution BVP and NDSolve solution with initial data only
Table[{.7 + i/10,
Table[Show[
Plot[sol1[[i + 1]][[s]][t], {t, 0, tmax}, PlotRange -> All],
Plot[Evaluate[
Sum[aa[i + 1, k, s] psi[i, k, t], {i, 0, M0}, {k, nn}] /.
ldgsol[i]], {t, 0, tmax}, PlotRange -> All,
PlotStyle -> {Red, Dashed}]], {s, ns}]}, {i, 0, kmax}]
Please note, that up to k=1.5 we have a good coincidence sol1 with ldgsol, but then solutions diverge, for example for k<1.5
 and for
and for k>1.5

Update 1. With option Method -> {"Newton", "StepControl" -> "TrustRegion"} for FindRoot we can extend solution to k=10.7, but there are oscillation around some points.

Code for this case
params = {a -> 0.4, m -> 2.4, Izz -> 1.0, g -> 9.81, fc -> 13.6829};
T = 2.0; kmax = 50;
Get["NumericalDifferentialEquationAnalysis`"];
UT[mm_, t_] := EulerE[mm, t];
M0 = 5; nn = 12; ns = 4; np = 5; tmax = 2;
y[t_] = Table[Symbol["y" <> ToString[i]][t], {i, 1, ns}];
eqs = {q'[t] == z[t],
z'[t] == (-a g m Sin[q[t]] - fc Tanh[k z[t]] + x[t])/(Izz + a^2 m),
p'[t] == (a g m Cos[q[t]] x[t])/(Izz + a^2 m),
x'[t] == -p[t] + (fc k Sech[k z[t]]^2 x[t])/(Izz + a^2 m)}; F =
Table[eqs[[i, 2]], {i, ns}]; var = {q[t], z[t], p[t],
x[t]}; ini = {0, 0, pb, xb}; bc2 = {8/10, 0}; ff =
Table[F /. Table[var[[i]] -> y[t][[i]], {i, ns}] /.
params /. {k -> (7 + 2 kap)/10}, {kap, 0, kmax}];
LDGODEs[M0_, nn_, ns_, np_, f_, ini_, tmax_, kap_] :=
Module[{dx = tmax/nn, A = Array[aa, {M0 + 1, nn, ns}]},
xl = Table[ l*dx, {l, 0, nn}];
psi[mm_, k_, t_] :=
Piecewise[{{UT[
mm, (2 t - xl[[k + 1]] - xl[[k]])/(xl[[k + 1]] - xl[[k]])],
xl[[k]] <= t <= xl[[k + 1]]}, {0, True}}];
gg = Table[
GaussianQuadratureWeights[np, xl[[i]], xl[[i + 1]]], {i, nn}];
dp = Table[
D[UT[mm, (2 t - xl[[k + 1]] - xl[[k]])/(xl[[k + 1]] - xl[[k]])],
t], {k, nn}];
rul = Table[
y[t][[i]] ->
Sum[aa[mm, k, i] psi[mm - 1, k, t], {mm, 1, M0 + 1}, {k, 1,
nn}], {i, ns}];
eq = Flatten[
Table[-Sum[
aa[i + 1, n,
ks] (Table[(psi[i, n, t] If[j == 0, 0,
dp[[n]] /. mm -> j]), {t, gg[[n]][[All, 1]]}] .
gg[[n]][[All, 2]]), {i, 0,
M0}] - (Table[(f[[ks]] /. rul) psi[j, n, t], {t,
gg[[n]][[All, 1]]}] . gg[[n]][[All, 2]]), {j, 0, M0}, {n,
1, nn}, {ks, ns}] +
Table[Sum[
aa[i + 1, n,
ks] (psi[i, n, xl[[n + 1]]] psi[j, n, xl[[n + 1]]]), {i, 0,
M0}] - Sum[
If[n < 2, ini[[ks]]/(M0 + 1),
aa[i + 1, n - 1, ks] psi[i, n - 1, xl[[n]]]] psi[j, n,
xl[[n]]], {i, 0, M0}], {j, 0, M0}, {n, 1, nn}, {ks, ns}]];
bc = Table[
Sum[aa[i + 1, k, s] psi[i, k, 2], {i, 0, M0}, {k, nn}] ==
bc2[[s]], {s, 1, 2}];
eqn = Table[eq[[k]] == 0, {k, Length[eq]}];
var = Join[Flatten[A], {pb, xb}];
soln = FindRoot[Join[eqn, bc],
Table[{var[[i]], If[kap == 0, 1/10, var[[i]] /. soln]}, {i,
Length[var]}],
Method -> {"Newton", "StepControl" -> "TrustRegion"}];
soln];
Do[
ldgsol[kap] =
LDGODEs[M0, nn, ns, np, ff[[kap + 1]], ini, tmax, kap];, {kap, 0,
kmax}] // AbsoluteTiming
Visualization
leg = {"q", "z", "p", "x"};
Table[Plot[
Evaluate[
Table[Sum[aa[i + 1, k, s] psi[i, k, t], {i, 0, M0}, {k, nn}] /.
ldgsol[kap], {kap, 0, kmax, 1}]], {t, 0, tmax}, PlotRange -> All,
PlotLegends -> Table[(7. + 2 n)/10, {n, 0, kmax, 1}],
Frame -> True, PlotLabel -> leg[[s]]], {s, ns}]




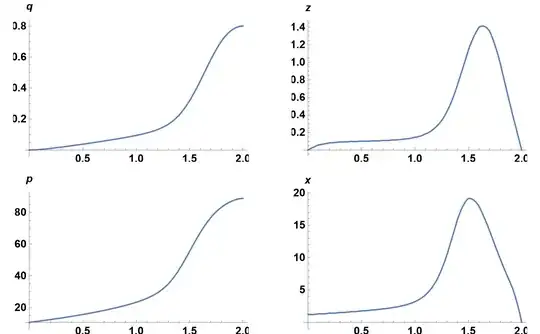





vars = {q, z, p, x}; varsF[t_] = Through[vars[t]];andMethod -> {"Shooting", "StartingInitialConditions" -> Thread[varsF[0] == (varsF[0] /. oldsolF[[1]])]}after saving a successfulsolFasoldsolF = solF. – Michael E2 Aug 31 '22 at 15:59k=3.7we have same message fromFindRootas above. Substituting data back inNDSolvewe can see thatNDSolvereproduces LDG solution up tok=1.5, and over `k=1.5 the solution deviates from LDG. – Alex Trounev Sep 01 '22 at 15:25NDSolve? I cannot find it in the documentation... Would you share your code? I think that already going up tok=3.6is a very good performance increase. – Meclassic Sep 01 '22 at 17:40NDSolve. It is not even mentioned in Mathematica while it widely use as an effective solver in combination with FEM for ODEs and PDEs. – Alex Trounev Sep 01 '22 at 19:04FindRootwith LDG. However, I understand that you coded that into Mathematica. Any chance that you could post your code as an alternative answer? – Meclassic Sep 01 '22 at 19:48