Slopefield curves for various points

Question

I want to find the Slopefield curve for the ODE

\begin{equation} y'=y^{2/3} \end{equation}

at the points given under.

In[72]:= ClearAll
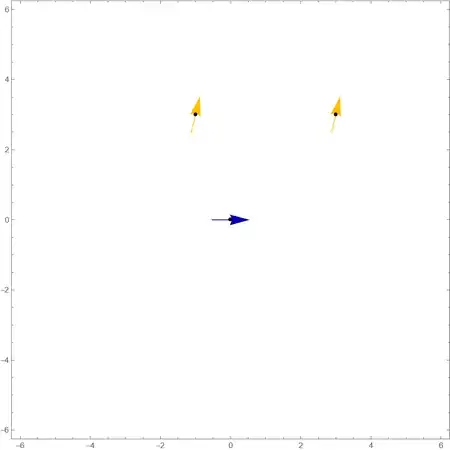
In[77]:= initvalues1 = {{0, 0}, {-1, 3}, {3, 3}}
Out[77]= {{0, 0}, {-1, 3}, {3, 3}}
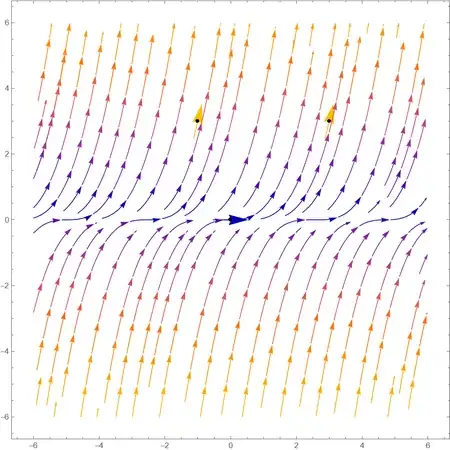
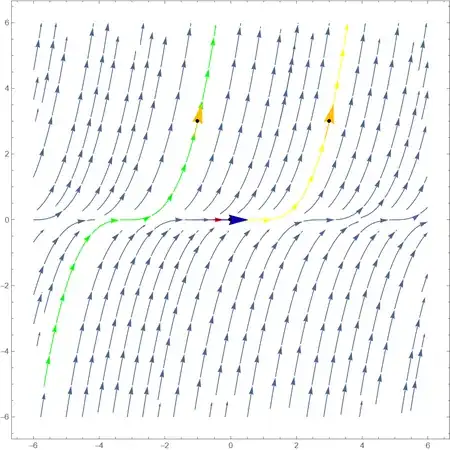
In[78]:= SlopeField[Evaluate[y' == 2 y^(2/3)], {y, -6., 6.}, {x, -6., 6.}, initvalues1]
Out[78]= SlopeField[
 1/27 (6 C[1]^2 + 24 C[1] #1 + 24 #1^2) & == 2 y^(2/3), {y, -6., 6.}, {x, -6.,
   6.}, {{0, 0}, {-1, 3}, {3, 3}}]

But I get no plot at all.

Any ideas why?

Thanks

As to "why?", compare output of Table[y^(2/3), {y, -1., 1., 0.5}] with that of Table[CubeRoot[y^2], {y, -1., 1., 0.5}] — Bob Hanlon, Sep 02 '22 at 14:27
I'm voting to close this question because: 1. As pointed out by @Daniel , definition of SlopeField is missing. 2. Even if the definition is added, this is probably a duplicate of https://mathematica.stackexchange.com/q/3886/1871 — xzczd, Oct 31 '22 at 12:04
BTW, ClearAll won't do what you're imagining, please read the document carefully. One correct wayto "clear all" is Clear@"`*". — xzczd, Oct 31 '22 at 12:05

cvgmt · Accepted Answer · 2022-09-02T13:07:46.163

Maybe use VectorPlot and CubeRoot for y^(1/3).

initvalues1 = {{0, 0}, {-1, 3}, {3, 3}};
VectorPlot[{1, 2 CubeRoot[y^2]}, {x, -6, 6}, {y, -6, 6}, 
 VectorPoints -> initvalues1, 
 Epilog -> {Black, PointSize[Medium], Point[initvalues1]}]

Or

StreamPlot[{1, 2 CubeRoot[y^2]}, {x, -6, 6}, {y, -6, 6}, 
 VectorPoints -> initvalues1, 
 Epilog -> {Black, PointSize[Medium], Point[initvalues1]}]

emphasize some lines

initvalues1 = {{0, 0}, {-1,3},{3,3}};
 colors = {Red, Green, Yellow};
 StreamPlot[{1, 2 CubeRoot[y^2]}, {x, -6, 6}, {y, -6, 6}, 
 VectorPoints -> initvalues1, 
 Epilog -> {Black, PointSize[Medium], Point[initvalues1]}, 
 StreamPoints -> {{Sequence @@ Thread[{initvalues1, colors}], 
    Automatic}}, StreamColorFunction -> None]

Slopefield curves for various points

1 Answers1