How do I solve the following cubic-quintic stochastic differential equation (Duffing equation)?
$$ \ddot{x} + \epsilon\gamma\delta \dot{x}-ax+bx^3+cx^5=\epsilon\gamma\delta \cos(\omega t) +\eta[t] $$
Here $\eta[t]$ is Gaussian white noise. The equation describes the stochastic motion of a particle in a harmonic potential. $\gamma$ is a modulation factor determining the relative strength of deterministic and stochastic forcings such that $0<\gamma<1$, let $a=1,b=-1,c=0,\omega=1.1$. The solution in the case $b=c=0$ is already discussed and solved as well in this question and its Ito is of the Stratonovic form. Really, I can't solve the above equation for $b\neq 0$ or for $c\neq 0$.For mathematica code ,I have tried to rewrite for $c=0$ the equations of motion for the harmonic oscillator as a system of first order equations such that $$ \dot{x}=v\\ \dot{v}=ax-bx^3-\gamma \epsilon v+A\cos(wt)+\eta(t),A=\gamma \epsilon $$ I have got solution of that problem in the case of absence of white noise term for some values of $a=1,b=-1$ and $\omega$ with $c=0$, let $A=0.2$ and with initial condition $x(0)=0,v(0)=0$ My code with absence of white Gaussian noise is :
Clear[A];
solution[A_, tmax_] := NDSolve[{v'[t] == x[t] - x[t]^3 - 0.05*v[t] + A*Cos[1.1*t],
x'[t] == v[t], x[0] == 0, v[0] == 0}, {x, v}, {t, 0, tmax}, MaxSteps -> 100*tmax]
sol3 = solution[0.2, 800]
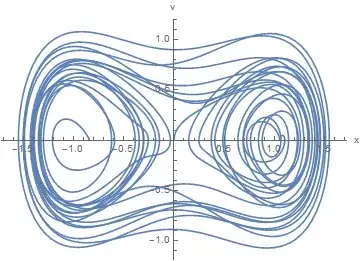
graph[tmin_, tmax_] := ParametricPlot[Evaluate[{x[t], v[t]} /. sol3],
{t, tmin, tmax}, AxesLabel -> {"x", "v"}]
graph[0, 200]
Now what about in the presence of white Gaussian noise where $\eta(t)\neq0$ , am not familar with stochastics case ? I want applying the mathematica code montioned in this question. EditI have an attempt to solve the titled coupled system using winer process(adding noise term) , I have got only PDF formula but i can't plot it .
My Code
A=1.3;b=a=1;c=0.05;m=1.4;x0=0; y0=1;
procNum =
ItoProcess[{\[DifferentialD]x[t] ==
y[t] \[DifferentialD]t, \[DifferentialD]y[t] ==
a*x - b*x^3 - c*y + A *Cos[m*t] \[DifferentialD]w[t]},
x[t], {{x, y}, {x0, y0}}, {t, 0}, w \[Distributed] WienerProcess[]]
Mean[procNum[t]]
Integrate[pdf[1, x], {x, -Infinity, Infinity}] // N
Plot[{pdf[1, x], pdf[5, x]}, {x, -5, 5}, PlotRange -> All]