Coarse-graining and/or sorting of a list of arbitrary triades {x,y,z} in the (x,y) plane

Question

In general my question is related to an approach to make an interpolation of a data which is not on a regular mesh. Another aspect of this question has already been discussed after my question "Numerical integration of a numeric data available as a nested list".

I have data in the form of a list of triads {x, y, z} that came from an external simulation. It may be and may be not ordered. Further, x and y lie within a rectangle R, and are not regularly spaced. I would like to coarse-grain and simultaneously sort this data. The coarse-graining consists in partitioning the rectangle R into multiple small rectangles and constructing a list {xij, yij, zij} where xij and yij are the coordinates of the centers of the rectangles, while zij is the average of all z values for which x and y belong to the rectangle specified by i and j. To be specific, let us build a list mimicking the real one, but small enough:

a = RandomReal[{0, 10}, {10000, 2}];
b = RandomReal[{-1, 1}, {10000}];
lst = 
  MapThread[Insert[#1, #2, 3] &, {a, b}] /. 
   {x_, y_, z_} -> {x, y, 10 Exp[-((x - 5)^2 + (y - 5)^2)/4] + z};

The list lst has 10000 elements with x and y located between 0 and 10. The coarse-grained list may be obtained by the averaging over squares with the sizes 0.5*0.5 like this:

lstCoarseGrained = Flatten[Table[
    (s = Select[
       lst, ((i <= #[[1]] <= i + 0.5) && (j <= #[[2]] <= j + 0.5) &)];
      {{i + 0.25, j + 0.25}, Mean[Transpose[s][[3]]]}),
    {i, 0, 9.75, 0.5}, {j, 0, 9.75, 0.5}], 1];

It has

Length[lstCoarseGrained]

400

elements and can be straightforwardly interpolated:

f = Interpolation[lstCoarseGrained, InterpolationOrder -> 3, Method -> "Spline"]

plotted:

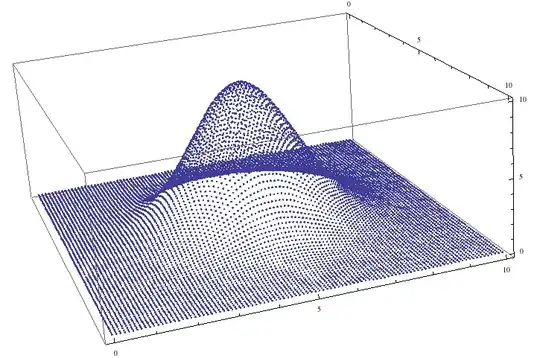
Row[{
  ListPlot3D[lst, PlotRange -> All, ImageSize -> 250], 
  Plot3D[f[x, y], {x, 0, 10}, {y, 0, 10}, PlotRange -> All, ImageSize -> 250]
}]

enter image description here

and then further post-processed. On the figure above the left image shows the data before, and the right - after the coarse-graining and interpolation.

However, the coarse-graining by this approach requires

Timing[
  Flatten[
    Table[
      (
        s = Select[lst, ((i <= #[[1]] <= i + 0.5) && (j <= #[[2]] <= j + 0.5) &)];
        {{i + 0.25, j + 0.25}, Mean[Transpose[s][[3]]]}
      ),
      {i, 0, 9.75, 0.5}, {j, 0, 9.75, 0.5}],
    1];]

{13.468750, Null}

13 seconds. My realistic lists have about 10^6 triads and will require about 21 min.

My question is, if you can see a faster way to do this?

In principle, if I could, say, use something like Partition instead of a Table, it would go faster. However, to do this, the list should be first sorted in 2D, and I do not see, how. So the second question is if you see the way to sort the list with elements {x,y,z} with arbitrary order in the (x,y) plane such that it is organized as like, say, the list given by the table:

Table[{i, j}, {i, 1, 5}, {j, 1, 5}]

In your definition of lst, you should use :> (RuleDelayed) rather than -> (Rule). A (faster) alternative here is MapThread[Append[#1,10 Exp[-((#1[[1]]-5)^2+(#[[2]]-5)^2)/4]+#2]&,{a,b}]. Just to show you that we have Append here rather than Insert[_,_,3], I realize is not the step you want to optimize. — Jacob Akkerboom, Jun 20 '13 at 11:28
@Jacob Akkerboom My question is not about speeding up making the table returning the list lst. This is a phony table I only generate for the sake of example. The question is how to speed up making the list lstCoarseGrained. — Alexei Boulbitch, Jun 20 '13 at 11:38
Alexei, if you disagree that this question is a duplicate of the one linked by Leonid, please state why. — Simon Woods, Jun 20 '13 at 13:17
just realised there is this discussion and the linked both works and is much faster. I'd agree this is a duplicate. — gpap, Jun 20 '13 at 15:02
As recommended by Leonid and supported by others I have closed this as a duplicate, and as Simon requested if you disagree please state why. — Mr.Wizard, Jun 20 '13 at 16:52
@Leonid, These two questions are, indeed, related, though they are not equal. The approach Optimising2Dbinningcode (see above) generates the nested list with the structure such as is created by Table[expr,{i..},{j..} ], while during the coarse-graining procedure one attributes the values averaged over some region to the coordinates of the central points of these regions obtaining the data structure: {...{Xregioncenter,Yregioncenter,Zaveragedoverregion}...}. However, once the binning is done, the further rearrangement into the list with the data structure is already a rather simple task. — Alexei Boulbitch, Jun 24 '13 at 11:46
@MrWisard. In this sense Optimising2Dbinningcode (almost) answers my question. There is, however, one aspect. The formulation of question in the article Optimising2Dbinningcode is done by a mathematician using the mathematical language. Mine is formulated on the physical language and references to the well-known and crucial coarse-graining procedure of physics, and might be of a general interest for physicists using Mma. When I saw the "mathematical formulation" for the first time I did not recognize its relevance to me. So, you were probably too fast to close this question. — Alexei Boulbitch, Jun 24 '13 at 11:56
@Alexei I'm embarrassed to have to say that I did not read your comment until now. Sorry. Are you aware that a closed question with a positive score, such as this one, will not be (automatically) deleted and intentionally serves the purpose of providing another entry point to the existing answers? Does that address your concern? — Mr.Wizard, Jul 30 '13 at 05:43
@Mr. Wizard No, I did not know that. Thank you for the explanation. — Alexei Boulbitch, Jul 31 '13 at 05:54

score 1 · Answer 1 · edited Apr 13 '17 at 12:55

Like in the example you link, I'd use Nearest.

Your $ 1000 \times 1000 $ data points:

a = RandomReal[{0, 10}, {1000000, 2}];
b = RandomReal[{-1, 1}, {1000000}];
lst = MapThread[
   Append[#1, 
     10 Exp[-((#1[[1]] - 5)^2 + (#[[2]] - 5)^2)/4] + #2] &, {a, b}];

and a $ 100 \times 100 $ grid

grid = Module[{xres, yres},
   xres = 100;
   yres = 100;
   Flatten[Table[N@{i, j}, {i, 0, 10, 10/xres}, {j, 0, 10, 10/yres}], 
    1]];

now write a nearest function:

Timing[nf = Nearest[Thread[lst[[All, 1 ;; 2]] -> lst[[All, 3]]]];]
(*OUT=*) {1.88471, Null}

which you can run so that it averages over the $ n $ (here 1000) nearest points in the $ x-y $ plane

Timing[interpolatable = ({Sequence @@ #, Mean@nf[#, 1000]} & /@ 
 grid);]
(*OUT=*) {6.93931, Null}

Much like a moving average you may lose some information if you oversmooth and also the metric in the nearest function isn't binning in rectangles. In fact if you change it, it will become much slower.

The new set, however, is both smooth and regularly spaced and my guess is, if you are averaging over lots of points you won't see much difference:

ListPointPlot3D[interpolatable, PlotRange -> All]

smooth set

Coarse-graining and/or sorting of a list of arbitrary triades {x,y,z} in the (x,y) plane

1 Answers1