I have been trying to solve a system of equations with Runge-Kutta Order 4th but when I tried to run it the answer I got is a big equation with the word List in it instead of an Array. I put n=2 because otherwise it will take the program a lot to load on my laptop.
Edit: Thanks to Nasser I don't have a problem with List but now I get as solutions some extremly big numbers. Is there a calculator online for system of equations like this or can someone tell me if its a problem with the code?
I replaced rho sigma and beta with v, j and c
Clear[f, g, u, k1, k2, k3, k4, v, i, j, c, l1, l2, l3, l4, p1, p2, \
p3, p4]
v = 28
j = 10
c = 3/8
n = 2
x = ConstantArray[0, n + 1]
y = ConstantArray[0, n + 1]
z = ConstantArray[0, n + 1]
t = ConstantArray[0, n + 1]
x[[1]] = 2
y[[1]] = 1
z[[1]] = 3
ti = 0
tf = 1
dt = (a + b)/n
t[[1]] = ti
x
y
z
f[x_, y_] := v(y - x)
g[x_, y_, z_] := x(j - z) - y
u[x_, y_, z_] := xy - cz
For[
i = 1, i <= n, i++,
k1 = f[x[[i]], y[[i]]];
l1 = g[x[[i]], y[[i]], z[[i]]];
p1 = u[x[[i]], y[[i]], z[[i]]];
k2 = f[x[[i]] + dt/2k1, y[[i]] + dt/2l1];
l2 = g[x[[i]] + dt/2k1, y[[i]] + dt/2l1, z[[i]] + dt/2 + p1];
p2 = u[x[[i]] + dt/2k1, y[[i]] + dt/2l1, z[[i]] + dt/2 + p1];
k3 = f[x[[i]] + dt/2k2, y[[i]] + dt/2l2];
l3 = g[x[[i]] + dt/2k2, y[[i]] + dt/2l2, z[[i]] + dt/2 + p2];
p3 = u[x[[i]] + dt/2k2, y[[i]] + dt/2l2, z[[i]] + dt/2 + p2];
k4 = f[x[[i]] + dtk3, y[[i]] + dtl3];
l4 = g[x[[i]] + dtk3, y[[i]] + dtl3, z[[i]] + dtp3];
p4 = u[x[[i]] + dtk3, y[[i]] + dtl3, z[[i]] + dtp3];
x[[i + 1]] = x[[i]] + (dt/6)(k1 + 2k2 + 2k3 + k4);
y[[i + 1]] = y[[i]] + (dt/6)(l1 + 2l2 + 2l3 + l4);
z[[i + 1]] = z[[i]] + (dt/6)(p1 + 2p2 + 2*p3 + p4);
t[[i + 1]] = t[[i]] + dt
]
x
y
z
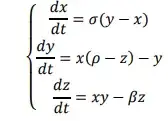



For[ i = 0,then dox[[i]]becausex[[0]]is the head, which isList. That is why you are gettingListeverywhere in your output . – Nasser Sep 06 '22 at 19:26NDSolveinstead. – xzczd Sep 07 '22 at 05:26