How to find the area locked between two curves and a line

Question

I need to find the area which is locked between these two curves and a line(the darker area). I have all three equation both curves and the line. enter image description here

I want just want to composite the right integral for this operation. I will evaluate the area.

Are you sure this Is about the software Wolfram Mathematica and not mathematics in general? — Lukas Lang, Sep 09 '22 at 12:43
Please post all of the functions by Mathematica code at first. — cvgmt, Sep 09 '22 at 12:51

score 9 · Answer 1 · answered Sep 09 '22 at 13:40

f1[x_] := 1/2*x + 3/2;
f2[x_] := 16/25*x^2 - 16/5*x + 4;
f3[x_] := 6/25*x^2 - 6/5*x + 3/2;

xp1 = x /. First@NSolve[f2[x] == f1[x] && 0 < x < 2.5, x]
yp1 = f1[xp1]

xp2 = 0;
yp2 = f3[xp2];

xp3 = 2.5;
yp3 = 0;

p1=Plot[{f1[x], f2[x], f3[x]}, {x, 0, 5}, 
 PlotLegends -> {"f1", "f2", "f3"}, GridLines -> Automatic, 
 GridLinesStyle -> LightGray, 
 Epilog -> {Red, PointSize[0.02], 
   Point[{{xp1, yp1}, {xp2, yp2}, {xp3, yp3}}]}]

Mathematica graphics

r1 = ImplicitRegion[y > f3[x] && y < f1[x], {{x, 0, xp1}, y}]
r2 = ImplicitRegion[y > f3[x] && y < f2[x], {{x, xp1, 2.5}, y}]
Area@RegionUnion[r1, r2]

Mathematica graphics

p2=RegionPlot[RegionUnion[r1,r2],PlotRange->{{0,5},{0,4}}]
Show[p1,p2]

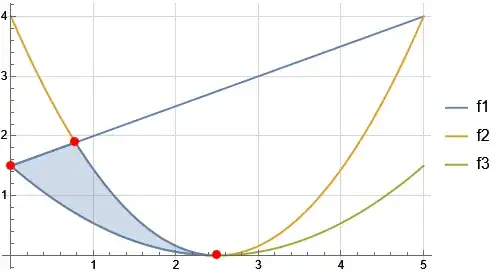
Mathematica graphics

cvgmt · Answer 2 · 2022-09-09T14:43:09.533

Thanks @Nasser work out all the formulas.

Clear[f1, f2, f3, plot, reg];
f1[x_] = 1/2*x + 3/2;
f2[x_] = 16/25*x^2 - 16/5*x + 4;
f3[x_] = 6/25*x^2 - 6/5*x + 3/2;
plot = Plot[{f1[x], f2[x], f3[x]}, {x, 0, 5}, 
   PlotStyle -> {Red, Green, Blue}];
reg = ImplicitRegion[{0 <= x <= 5/2, f3[x] <= y <= f2[x], 
    y <= f1[x]}, {x, y}];
reg // Area
Show[plot, 
 RegionPlot[DiscretizeRegion@reg, PlotStyle -> Orange, 
  BoundaryStyle -> Thick]]

14225/12288

Or

x0 = SolveValues[{f1[x] == f2[x], 0 <= x <= 5/2}, x][[1]]
(* 25/32 *)
Integrate[f1[x] - f3[x], {x, 0, x0}] + 
 Integrate[f2[x] - f3[x], {x, x0, 5/2}]

14225/12288

score 3 · Answer 3 · answered Sep 09 '22 at 18:01

Use ResourceFunction:

f1[x_] = 1/2*x + 3/2;
f2[x_] = 16/25*x^2 - 16/5*x + 4;
f3[x_] = 6/25*x^2 - 6/5*x + 3/2;
x1 = x /. Solve[f1[x] == f2[x], x] // First;
x2 = x /. Solve[f2[x] == f3[x], x] // First;
area1 = ResourceFunction["AreaBetweenCurves"][{f1[x], f3[x]}, {x, 0, x1}];
area2 = ResourceFunction["AreaBetweenCurves"][{f2[x], f3[x]}, {x, x1, x2}];
area = area1 + area2
14225/12288
area // N
1.15763

How to find the area locked between two curves and a line

3 Answers3