Kernel quits upon computing RegionIntersection

Question

Using 12.1.1.0 on MacOS BigSur I observe quitting Mathematica kernels when evaluating RegionIntersections on two regions that apparently only touch.

Example for Regions that cause the Kernel to quit without throwing error messages:

RegionIntersection[ 
 Polyhedron[{{-14.481838045552937`, -3.8913713702921195`, 
    13.743481930417099`}, {-13.387327710535084`, -4.686579676023987`, 
    14.579613424294676`}, {-13.592704266151834`, -3.145108820945274`, 
    14.801904645288225`}, {-12.786161768700419`, -4.476126018218702`, 
    13.92490718079964`}, {-12.982315767496441`, -3.0038758320024415`, 
    14.137216281827229`}, {-13.831522463803132`, -3.716627016121334`, 
    13.126322670747593`}}, {{1, 2, 3}, {5, 4, 6}, {4, 5, 3, 2}, {3, 5,
     6, 1}, {4, 2, 1, 6}}], 
 Cuboid[{-13.2`, -6.`, 14.375`}, {-10.8`, -3.5999999999999996`, 
   15.625`}]]

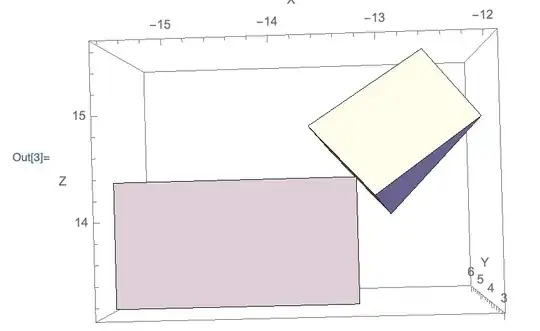
These are the regions:

When I only slightly change the coordinates to get regions that either overlap or do not overlap at all, I get the intersection polyhedron or the empty region indicator instead.

These are the regions that do overlap

RegionIntersection[ 
 Polyhedron[{{-14.481838045552937`, -3.8913713702921195`, 
    13.743481930417099`}, {-13.387327710535084`, -4.686579676023987`, 
    14.579613424294676`}, {-13.592704266151834`, -3.145108820945274`, 
    14.801904645288225`}, {-12.786161768700419`, -4.476126018218702`, 
    13.92490718079964`}, {-12.982315767496441`, -3.0038758320024415`, 
    14.137216281827229`}, {-13.831522463803132`, -3.716627016121334`, 
    13.126322670747593`}}, {{1, 2, 3}, {5, 4, 6}, {4, 5, 3, 2}, {3, 5,
     6, 1}, {4, 2, 1, 6}}], 
 Cuboid[{-13.25`, -6.`, 14.375`}, {-10.75`, -3.5999999999999996`, 
   15.625`}]]

with the corresponding output:

and the corresponding 3D graphics:

These are the regions that do not overlap

RegionIntersection[ 
 Polyhedron[{{-14.481838045552937`, -3.8913713702921195`, 
    13.743481930417099`}, {-13.387327710535084`, -4.686579676023987`, 
    14.579613424294676`}, {-13.592704266151834`, -3.145108820945274`, 
    14.801904645288225`}, {-12.786161768700419`, -4.476126018218702`, 
    13.92490718079964`}, {-12.982315767496441`, -3.0038758320024415`, 
    14.137216281827229`}, {-13.831522463803132`, -3.716627016121334`, 
    13.126322670747593`}}, {{1, 2, 3}, {5, 4, 6}, {4, 5, 3, 2}, {3, 5,
     6, 1}, {4, 2, 1, 6}}], 
 Cuboid[{-13.15`, -6.`, 14.375`}, {-10.85`, -3.5999999999999996`, 
   15.625`}]]

The output here is EmptyRegion, and the corresponding 3D graphics is:

Welcome to the Mathematica Stack Exchange. It is a good question, but it requires some editing. — Syed, Sep 11 '22 at 13:20
The problem is trying to do a subtle calculation using machine precision. Rationalize the numeric values prior to calculation. — Bob Hanlon, Sep 11 '22 at 14:37
Thanks for the correction of the editing @Syed! At the beginning it looked good for me in the preview, but then when I posted it, the images were gone. Was the first time I posted something. Hopefully next time I manage without syntax errors. — Christoph lerche, Sep 12 '22 at 14:28
Thanks for the suggestion @bobhanlon . I tried it, but with out success. Although, It would be helpful if a message was issued with this hint, instead producing a quitting kernel. Triggered by your comment, I tried to reduce the precision with Round[] (as RegionIntersection has no option for modifying this). This at least prevents the kernel from quitting. It does not evaluate the command, but I can catch this case with Head[] or similar. Fortunately, I can go ahead with rather low precision, so this work-around does the job for me. — Christoph lerche, Sep 12 '22 at 14:58
Oh, yes, just saw now that it was done by him. Thanks a lot for the editing, @marcob . — Christoph lerche, Sep 12 '22 at 15:04
A kernel crash like this represents a bug, and cannot be fixed by the people who visit this site. It can only be fixed by Wolfram Research, and they will only fix it if someone reports it to them. See How to report a bug in Mathematica — Jason B., Sep 12 '22 at 15:09
Thanks for the hint @JasonB . Until now, I was only suspecting it could be a bug, but I was not sure. I will report to Mathematica as indicated. — Christoph lerche, Sep 12 '22 at 15:22

score 1 · Answer 1 · answered Sep 12 '22 at 15:42

Here are examples with v12.1.1 using exact values rather than machine precision

$Version
(* "12.1.1 for Mac OS X x86 (64-bit) (June 19, 2020)" *)
Clear["Global`*"]
rgn1 = Polyhedron[{{-14.481838045552937, -3.8913713702921195, 
      13.743481930417099}, {-13.387327710535084, -4.686579676023987, 14.579613424294676}, {-13.592704266151834, -3.145108820945274, 
      14.801904645288225}, {-12.786161768700419, -4.476126018218702, 13.92490718079964}, {-12.982315767496441, -3.0038758320024415, 
      14.137216281827229}, {-13.831522463803132, -3.716627016121334, 13.126322670747593}} // 
    Rationalize[#, 0] &, {{1, 2, 3}, {5, 4, 6}, {4, 5, 3, 2}, {3, 5, 6, 
     1}, {4, 2, 1, 6}}];
rgn2 = Cuboid @@ 
   Rationalize[{{-13.2, -6., 14.375}, {-10.8, -3.5999999999999996, 15.625}}, 0];
rgn3 = RegionIntersection[rgn1, rgn2];
Volume[rgn3]
(* 3.9150410^-8 )
rgn4 = Cuboid @@ 
   Rationalize[{{-13.25, -6., 14.375}, {-10.75, -3.5999999999999996, 15.625}}, 0];
rgn5 = RegionIntersection[rgn1, rgn4];
Volume[rgn5]
(* 0.00139939 *)

Thanks @bobhanlon . I was not aware of the second argument for Rationalise[]. This did the job. Thanks! — Christoph lerche, Sep 13 '22 at 07:31
Unfortunately, there is another combination of regions with similar problems, and I'm not able to fix it with Rationalise[]. The description is in the Answer below, since characters for comment are too limited. — Christoph lerche, Sep 13 '22 at 19:27

score 1 · Answer 2 · answered Sep 13 '22 at 19:46

I observe a very similar behaviour with the following two regions:

When I try to run RegionIntersection on these regions, the computation takes more than 30 minutes. (I quit the kernel after this time, since for all other region pairs that I need to compute, the computations takes much less than a second). This is the corresponding command:

RegionIntersection[ 
 Cuboid[Rationalize[{-15.599999999999998`, 3.5999999999999996`, 
    13.125`}, 0], Rationalize[{-13.2`, 6.`, 14.375`}, 0]], 
 Polyhedron[
  Rationalize[{{-12.506721429921425`, 3.9624773092852443`, 
     15.656022698345078`}, {-13.443519981142686`, 4.706251231025362`, 
     14.640810221789032`}, {-13.649758588935882`, 3.158310171489477`, 
     14.864034492956131`}, {-12.837481483332462`, 4.494091809209582`, 
     13.980797468731524`}, {-13.034422783855483`, 3.0159324642645027`,
      14.193958713089975`}, {-11.942914132535591`, 3.783847471304209`,
      14.950243818178507`}}, 
   0], {{1, 2, 3}, {5, 4, 6}, {4, 5, 3, 2}, {3, 5, 6, 1}, {4, 2, 1, 
    6}}]]

Now, when I change the order of the Polyhedron and the Cuboid, I get an output, i.e. the kernel does not hang or stuck in the computation, but I don't get the desired result. Instead, I get:

The command that produces this output is:

RegionIntersection[
 Polyhedron[
  Rationalize[{{-12.506721429921425`, 3.9624773092852443`, 
     15.656022698345078`}, {-13.443519981142686`, 4.706251231025362`, 
     14.640810221789032`}, {-13.649758588935882`, 3.158310171489477`, 
     14.864034492956131`}, {-12.837481483332462`, 4.494091809209582`, 
     13.980797468731524`}, {-13.034422783855483`, 3.0159324642645027`,
      14.193958713089975`}, {-11.942914132535591`, 3.783847471304209`,
      14.950243818178507`}}, 
   0], {{1, 2, 3}, {5, 4, 6}, {4, 5, 3, 2}, {3, 5, 6, 1}, {4, 2, 1, 
    6}}], Cuboid[
  Rationalize[{-15.599999999999998`, 3.5999999999999996`, 13.125`}, 
   0], Rationalize[{-13.2`, 6.`, 14.375`}, 0]]]

Kernel quits upon computing RegionIntersection

2 Answers2