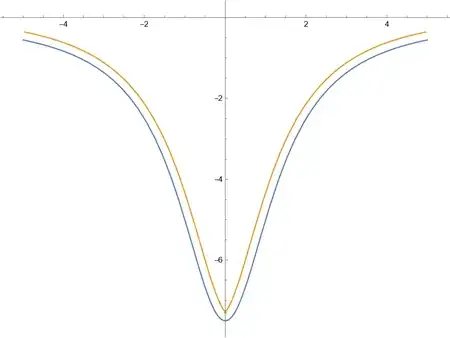
I would like to obtain a curve that is parallel to the function:
y(x) = -a/(x^2 + b)
I have tried to calculate the said curve by solving parametric equations, but as I tried to return to the Cartesian coordinates, the Eliminate instruction seems not to work (does not converge):
Assuming[{a > 0, b > 0, d > 0},
Eliminate[x == t + (2 a d t)/((b + t^2)^2 Sqrt[1 + (4 a^2 t^2)/(b + t^2)^4]) &&
y == -(a/(b + t^2)) - d/Sqrt[1 + (4 a^2 t^2)/(b + t^2)^4], t]],
where d is the distance between the curves.
Is there an alternative way to obtain a curve that is parallel to the given function in Cartesian coordinates using Mathematica?
Thank you!