10

So the following on social media recently makes me wonder - What is the most elegant way to create a table of rank-1 decompositions of country flags in Mathematica?

enter image description here

Edit

The question is vague, but a nice side-effect would be a pedagogical visualization of rank-1 decomposition using flags

Following Michael's solution gives something like this

enter image description here

Yaroslav Bulatov
  • 7,793
  • 1
  • 19
  • 44
  • You could apply your preference of decomposition to e.g. ImageData@ColorNegate@Binarize@CountryData["Austria", "Flag"]. – MarcoB Sep 15 '22 at 18:20
  • 3
    I do not know if other members have the same issue but I personally do not understand the decomposition in the image. For example, I do not understand why there is orange in the blue flag. – userrandrand Sep 15 '22 at 18:34
  • 1
    @userrandrand I think it's because blue + blue = 2 and you need a dummy variable/color for -1 to get blue + blue + orange = 1 or blue + orange = 0. Somewhat like the Inclusion-Exclusion Principle. – Michael E2 Sep 16 '22 at 12:18
  • @MichaelE2 Thank you. I think I understand now, the 2 d images/flags are represented as matrices, the colored bars are vectors, the terms in the decomposition are outer products of vectors and the orange is somewhat arbitrarily defined as the opposite of blue under this matrix representation. The only thing I don't understand now is why the mathematical translation was not added to the question. – userrandrand Sep 16 '22 at 19:51
  • @userrandrand I agree. Currently, it's perhaps closer to a puzzle than a clear question. – Michael E2 Sep 16 '22 at 22:33
  • The flag from Greece is rank 3 why are there so many terms ? Also the flags do not look like they add correctly. The last blue flag in the decomposition seems to be fully blue so assuming blue=1 and white=0, there can not be any white in the output of the sum as the matrices have positive coefficients – userrandrand Sep 18 '22 at 13:42
  • I saw the comment about quantization noise in MichaelE2's answer. I did not find too much noise with the Greek flag using ImageData@ColorNegate@Binarize@CountryData["Greece", "Flag"] as suggested by the first comment. Using that method, the flag from Switzerland has a bit of noise however. – userrandrand Sep 18 '22 at 13:52

3 Answers3

13

Using SmithDecomposition on @Roman's Greek flag (no need for orange with this method):

m={
 {1,1,1,1,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},
 {1,1,1,1,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},
 {1,1,1,1,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
 {1,1,1,1,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
 {0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},
 {0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},
 {1,1,1,1,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
 {1,1,1,1,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
 {1,1,1,1,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},
 {1,1,1,1,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},
 {0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
 {0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
 {1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},
 {1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},
 {0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
 {0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
 {1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},
 {1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1}};

{u, r, v} = SmithDecomposition[m];
u = Inverse[u]; v = Inverse[v];
cr = ColorRules -> {0 -> White, 
    1 -> First@DominantColors@CountryData["Greece", "Flag"]};
decomp = Sum[Inactive[Dot][u[[All, {j}]], v[[{j}]]],
   {j, Total@Diagonal@r}];
decomp /. a_?MatrixQ :> ArrayPlot[a, cr]
ArrayPlot[Activate@decomp, cr]
Michael E2
  • 235,386
  • 17
  • 334
  • 747
  • 1
    Very nice, Michael! I was suspecting that the LinearProgramming objective was suboptimal, and you've demonstrated it. – Roman Sep 17 '22 at 05:15
  • (+1) Wonderfull! – cvgmt Sep 17 '22 at 08:35
  • Quite a nice usage of SmithDecomposition which I learned about thanks to this answer. For approximating complicated higher rank flags, one possibility would be to truncate the singular value decomposition and then apply this SmithDecomposition. – userrandrand Sep 17 '22 at 18:17
  • Removing singular values that contribute less than 3 percent to the image, the above suggestion in code could be: {us,rs,vs}=SingularValueDecomposition[N@m]; cm=us . Threshold[rs,0.03*Total@Diagonal@rs] . ConjugateTranspose[vs]; bcm=ImageData@Binarize@Image@cm; {u, r, v} = SmithDecomposition[bcm];... – userrandrand Sep 17 '22 at 18:22
  • However, the suggestion above seems to require more terms than a direct singular value decomposition. For example with the flag from Canada and using the 3 percent threshold, reducing the number of terms in the decomposition roughly by two (24 instead of 47) leads to an image that looks more compressed than using 8 terms from the singular value decomposition. Nevertheless, the Smith decomposition looks more crisp even in that case. – userrandrand Sep 17 '22 at 18:28
  • 1
    @userrandrand As we noted in comments on the OP, the problem intended by the meme is unclear. If you're trying to approximate the matrix, then you're solving a different problem than I am. (The Smith decomposition can't be used to approximate.) The SVD was the first thing I thought of (+1 to your answer already), but I rejected because I thought finding an exact decomposition into integer matrices was the problem, and for low-rank matrices only, which seems clearly implied. I was able to use the SVD to get an integer decomposition on a couple of examples. It's ad hoc and I abandoned the idea. – Michael E2 Sep 17 '22 at 19:33
  • Agreed your answer definitely fits the question much better. My comments were mainly a side note for anyone reading in the future that might want to play with the answer you gave on higher rank matrices or for school projects for their country's flag. Since the idea is to have a simple decomposition it could be good to first reduce the rank via SVD in such cases which was why I added the comment. Thanks again for the help and for introducing the Smith decomposition to some of us (:. – userrandrand Sep 17 '22 at 19:51
  • Neat solution! This gives a good way to explain SVD. Decompositions of all simple 2 color flags looks like this (note, greece looks a bit different because of quantization noise) -- https://www.wolframcloud.com/obj/yaroslavvb/Published/twitter-flag%20decompositions.nb – Yaroslav Bulatov Sep 17 '22 at 23:34
7

What I understood from the question:

The 2 dimensional images/flags are represented by matrices according to their x-y pixel intensity. The colored bars are represented as vectors and each term in the decomposition is an outer product of vectors. The orange in the Greek flag is somewhat arbitrarily defined as the opposite of blue under this matrix representation.

To motivate the following, I will focus on a flag that requires many more terms in the decomposition to explore approximations/compressions of a given flag. The more pedagogical case of the flag from Switzerland will be given at the end.

I will consider first the Canadian flag as representing the maple leaf requires many terms but the flag is still simple enough that it can be identified from its compressed form shown below.

Getting the flag :

flag=CountryData["Canada","Flag"];

Extracting image data from the flag: (from the comments below OP's question)

m = ImageData@ColorNegate@Binarize@flag;

As mentioned above, the objective now is to obtain m as the sum below:

$$ m=\sum_{k}{u_k v_k^T} $$

Such a decomposition is given immediately by the singular value decomposition (sort of generalized eigenvalue decomposition) of m after rescaling the left and right singular vectors in such a way that they absorb the singular values of m in the usual decomposition. One caveat is that the components of u and v are fractional in general. It is unclear to me whether the question by OP imposes that the vectors should be integer or whether there is some simplicity constraint.

Obtaining the singular value decomposition of the flag:

{u, s, v} = SingularValueDecomposition[N@m];

To approximate the flag, I will consider only singular values whose fractional weight is above some threshold. Taking for example the treshold to be 2 percent, I will only consider singular values s[[j,j]] such that:

s[[j,j]]/Total@Diagonal[s] < 0.02

Under that constraint we have a maximal number of terms in the decomposition that verifies:

max = Max@Flatten@Position[Diagonal[s]/Total[Diagonal[s]], _?(# > 0.02 &)]

Output : (*8*)

Defining a graphical representation of the outer product:

outterProdTerm[index_] := Row[MatrixPlot[#, Frame -> False, ColorFunction -> "TemperatureMap"] & /@ {Transpose@{Sqrt[s[[index, index]]]*
   u[[All, index]]}, {Sqrt[s[[index, index]]]*v[[All, index]]}},"\[TensorProduct]"]

We can then obtain the decomposition of the image using temperature map colors where blue represents negative values and red represents positive values:

Row[outterProdTerm/@Range[max],"+"]

Output: decomposition

Next we perform the outer products. The example above might be too hard to follow but blue times blue is red since negative times negative is positive. In a similar manner, red times blue is blue. We define the following function that performs the outer products:

term[index_] := MatrixPlot[s[[index, index]]*
  KroneckerProduct[u[[All, index]], v[[All, index]]], Frame -> False,
  ColorFunction -> "TemperatureMap"]

Performing the outer products:

Row[term/@Range[max],"+"]

Output: decomposition2

Finally to add up the terms, we first set the variable "decomposition" below to be the list of terms in the decomposition. Defining the list before summing the terms could be useful if we want to do something with the terms as well.

decomposition = Table[s[[j, j]]*KroneckerProduct[u[[All, j]], v[[All, j]]], {j, 
max}];

The result of adding the leading singular value terms:

MatrixPlot[Total@decomposition//Chop]

Output:

compressed_version_of_canadian_flag

A more pedagogical example to understand the decomposition:

In this last section we consider the case of the flag from Switzerland that lends itself more easily to an analysis of the singular value decomposition. We will use the same functions as above except that now we will consider all the terms using:

max = Max@Flatten@Position[Diagonal[s]/Total[Diagonal[s]], _?(# != 0 &)]

The flag :

flag

Singular value decomposition:

decomposition_s

Calculating the outer products (blue*blue=red, red*blue=blue, red*red=red)

decomposition_s_2

Adding the terms above leads to the flag using red+blue=0 :

animate_add

userrandrand
  • 5,847
  • 6
  • 33
6

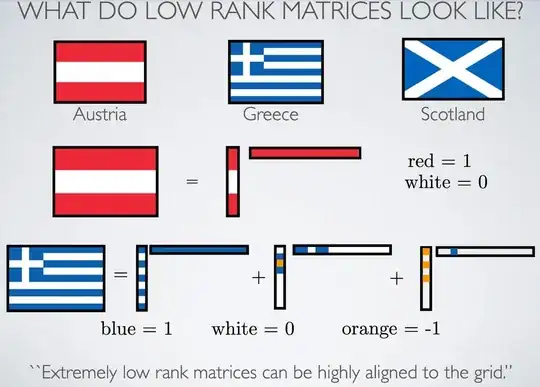
Here's a way to use linear programming to get reasonably simple solutions. As an example, I'll do the Greek flag.

The flag is defined as a 18×27 matrix:

M = {{1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
     {1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
     {1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
     {1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
     {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
     {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
     {1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
     {1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
     {1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
     {1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
     {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
     {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
     {1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
     {1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
     {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
     {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
     {1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
     {1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1}};
ArrayPlot[M, ColorRules -> {0 -> White, 1 -> RGBColor["#004C98"]}, PlotRangePadding -> None]

enter image description here

We have many duplicate rows and columns in this flag, so let's restrict problem-solving to unique rows/columns, giving a reduced 5×3 flag to be expressed in terms of outer products:

M1 = M // Transpose // DeleteDuplicates // Transpose // DeleteDuplicates
(*    {{1, 0, 1}, {1, 0, 0}, {0, 0, 1}, {0, 0, 0}, {1, 1, 1}}    *)
{py, px} = Dimensions[M1]
(*    {5, 3}    *)

Let's make a list of all possible Kronecker products of a binary 5-list with a binary 3-list. The flag will be expressed as a linear combination of such Kronecker products. Each Kronecker product can appear with a positive or negative sign. This is different from the OP's solution that uses contributions $\{-1,0,1\}$ and therefore finds a simpler solution. However, the present method can be extended to do this as well, I think.

p = Tuples[{{-1, 1}, Rest[Tuples[{0, 1}, py]], Rest[Tuples[{0, 1}, px]]}];
q = SparseArray[Flatten[#[[1]]*KroneckerProduct[#[[2]],#[[3]]]] & /@ p];

Find the linear combination of Kronecker products (in q) that (i) has the fewest contributing terms, (ii) has every term's prefactor restricted to $[0,1]$, and (iii) sums to express the reduced flag M1: the parameters given to LinearOptimization are

  1. the linear objective to be minimized: the sum of all term prefactors
  2. the linear inequality constraints: every prefactor must be in $[0,1]$
  3. the linear equality constraints: the terms must add up to M1.

Expressed in matrix form,

s = LinearOptimization[
      ConstantArray[1, Length[q]],
      {Join[IdentityMatrix[Length[q], SparseArray], -IdentityMatrix[Length[q], SparseArray]],
       Join[ConstantArray[0, Length[q]], ConstantArray[1, Length[q]]]},
      {Transpose[q], -Flatten[M1]}]
(*    {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 1/3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1/3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1/3, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       1/3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1/3, 0, 0, 0, 0, 0, 0, 1/3, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1/3, 0, 0,
       0, 0, 0, 0, 1/3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}    *)

Note that for larger problems, this optimization will be done numerically using, for example, an interior-point method.

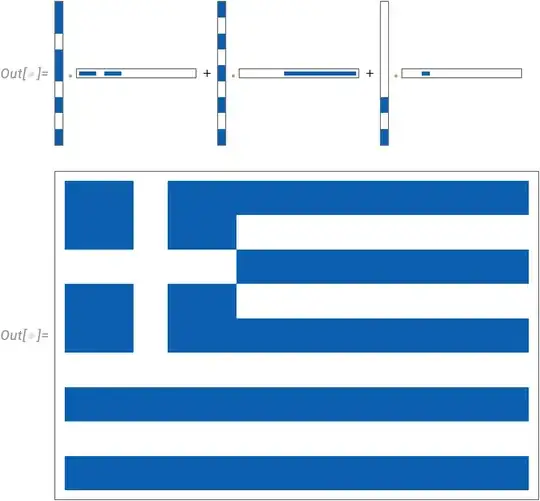
The resulting combination is quite sparse, containing only 8 terms:

f = s . ((#[[1]] kp[#[[2]], #[[3]]]) & /@ p)
(*    1/3 kp[{0, 0, 1, 0, 1}, {0, 1, 1}] +
      1/3 kp[{0, 1, 0, 0, 1}, {1, 1, 0}] +
      1/3 kp[{1, 0, 0, 0, 1}, {1, 1, 1}] +
      1/3 kp[{1, 0, 1, 0, 0}, {0, 0, 1}] +
      1/3 kp[{1, 0, 1, 0, 1}, {0, 0, 1}] +
      1/3 kp[{1, 1, 0, 0, 0}, {1, 0, 0}] +
      1/3 kp[{1, 1, 0, 0, 1}, {1, 0, 0}] -
      1/3 kp[{1, 1, 1, 0, 0}, {0, 1, 0}]      *)

where kp is a Kronecker product. Expanding the result to the full 18×27 flag:

F = f /. kp[{y1_, y2_, y3_, y4_, y5_}, {x1_, x2_, x3_}] -> 
         kp[{y1, y1, y2, y2, y3, y3, y2, y2, y1, y1, y4, y4, y5, y5, y4, y4, y5, y5},
            {x1, x1, x1, x1, x2, x2, x1, x1, x1, x1, x3, x3, x3, x3, x3, x3, x3, x3, x3, x3, x3, x3, x3, x3, x3, x3, x3}]

(*    1/3 kp[{0,0,0,0,1,1,0,0,0,0,0,0,1,1,0,0,1,1},
             {0,0,0,0,1,1,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1}] +
      1/3 kp[{0,0,1,1,0,0,1,1,0,0,0,0,1,1,0,0,1,1},
             {1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0}] +
      1/3 kp[{1,1,0,0,0,0,0,0,1,1,0,0,1,1,0,0,1,1},
             {1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1}] +
      1/3 kp[{1,1,0,0,1,1,0,0,1,1,0,0,0,0,0,0,0,0},
             {0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1}] +
      1/3 kp[{1,1,0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,1},
             {0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1}] +
      1/3 kp[{1,1,1,1,0,0,1,1,1,1,0,0,0,0,0,0,0,0},
             {1,1,1,1,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0}] +
      1/3 kp[{1,1,1,1,0,0,1,1,1,1,0,0,1,1,0,0,1,1},
             {1,1,1,1,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0}] -
      1/3 kp[{1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0},
             {0,0,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0}]    *)

Check that this sum of eight Kronecker products indeed reproduces the flag M:

(F /. kp -> KroneckerProduct) == M
(*    True    *)

Graphical representation of the solution:

Expand[3 F] /. kp[u__] :> ArrayPlot[KroneckerProduct[u], PlotRangePadding -> None]

enter image description here

Roman
  • 47,322
  • 2
  • 55
  • 121