The 1D wave equation is $$\frac{\partial^2 u(x,t)}{\partial t^2} = c^2 \frac{\partial^2 u(x,t)}{\partial x^2}$$ where $c$ is the wave speed, $c^2=E/\rho$, $E$ is the Young's modulus and $\rho$ is the density of the material. See the link. I want to analyze the physics in this video of longitudinal wave. When a mass impacts one end of a long rod with the material properties of $E$ and $\rho$ at $x=0$, longitudinal waves will be generated. Please note the $\textbf{initial conditions}$: $$v(x,t)=\dot{u}(x,t)=0$$ $$u(x,0)=0$$ where $v(x,t)$ represents the particle velocity in the medium. The $u(x,t)$ should be zero at time $t=0$.
Note that for any given time $0<t_1< L/c$, the longitudinal waves will travel to $$x_1=c\cdot t_1$$ For $x\geq x_1$, it is required that $$v(x,t_1)=0$$ $$u(x,t_1)=0$$ The waves will travel through the rod to the other end. Assume the length of the rod is $L$. The wave speed is $c$. At time $t=L/c$ the waves will reach $x=L$. Depending on the conditions and the other end, the waves can change and then be reflected.
- Free end condition. That is to say, there is nothing in contact with the other end (That is $x=L$). The particle in the medium can move in the free end. What will happen when the wave reaches there?
- Fixed end condition. In this condition, the particles in the medium at the fixed end cannot move. The particle velocity in the fixed end is strictly zero when the waves travel $x=L$. What will happen in the fixed end?
How should I analyze the two case scenarios for the 1D wave equation in Mathematica? I want to see how $u(x,t)$ will vary over $t$ and $x$.
Thank you very much!
Edited on 10/07/2022: Using the solution from Ulrich Neumann, the following animation presents the results.I have a question. Why will the $u(x,t)$ increase over time? I did not expect that.

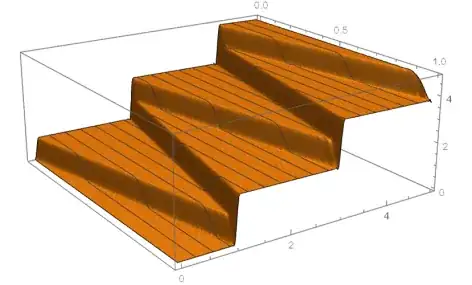

u[0,t]==0, Derivative[0,1][u][x,t]==0 and impact at x==0! – Ulrich Neumann Oct 07 '22 at 06:44NDSolveValu[...]you'll find the condition(*u[t,1]\[Equal]0,*)for fixed end. Remove comment and you get solution for fixed end. – Ulrich Neumann Oct 07 '22 at 14:42