How to find the Shortest Path, visiting ALL vertices, without coming back to the start (Hamiltonian Path, minimum distance)

Question

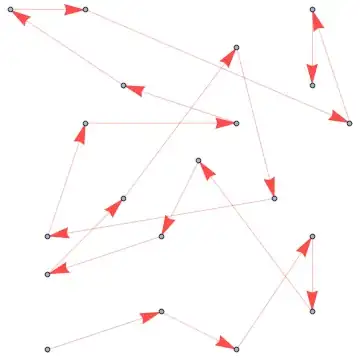
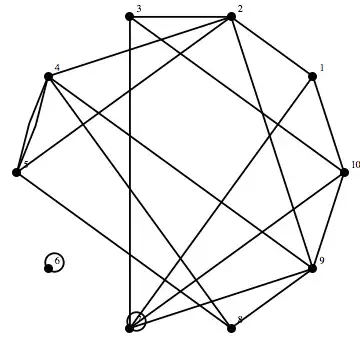
A car has to pick up each person and take them to their destination. I am trying to find the shortest tour that will do this. How can I find the shortest path between any s and t.... visiting all vertices, and without coming back to the start?

In this case I have 10 points. After each For[], I obtain an array with the distances from i to j.

t = {
  {{2, 1}, {5, 2}},
  {{7, 1}, {9, 4}},
  {{9, 2}, {6, 6}},
  {{5, 4}, {2, 3}},
  {{4, 5}, {7, 9}},
  {{8, 5}, {2, 4}},
  {{3, 7}, {7, 7}},
  {{4, 8}, {1, 10}},
  {{3, 10}, {10, 7}},
  {{9, 10}, {9, 8}}
  }
(* t[[i,j,k]    i\[Rule]Trip Nºi    j\[Rule] \
1=Inicio=Pick-Up  2=Fin=Drop-Off     k\[Rule] 1ª o 2ª componente (es \
decir x ó y) *)

Array[t2t, {10, 10}]
For[i = 1, i <= 10, i++,
 For[j = 1, j <= 10, j++,
  If[i != j,
   t2t[i, j] = 
        Sqrt[(t[[j, 1, 1]] - t[[i, 2, 1]])^2 + 
        (t[[j, 1, 2]] - t[[i, 2, 2]])^2], t2t[i, j] = Infinity
   (* In t2t there is the distance from i to j 
      different from distance from j to i, in general *)
   ]
  ]
 ]

I want to find the shortest tour through the 10 vertices, with the weight/distsances t2t[i,j] visiting all vertices, and not coming back to the start.

-- After comments on March´2015 I add the original problem published in ORMS magazine -- Now this kind of puzzles are published in Amalytics ( for example electriying in page 74 http://viewer.zmags.com/publication/79b53367#/79b53367/74 )

Answer 1

EDIT 1

Now that the question is getting more specific, here another approach:

I'd like to say that this is not a solution, but it shows you how to set-up your graph accordingly. If you combine this with the comment of @Rahul Narain you should get your result easily.

1) Create a PathGraph from the coordinates, with arrow edge style:

arrow[coord_, e_] := Style[Arrow[coord], Red, Thickness[.001], Arrowheads[0.06]]
pg = PathGraph[Range[Length@t], VertexCoordinates -> t, EdgeShapeFunction -> arrow]

2) Create a 10x10 grid:

gg = GridGraph[{10, 10}]

3) Overlay both graphs:

Overlay[{gg, pg}]

4) Let's find the shortest Tour and pick this tour from the coordinate list:

tour = t[[Last[FindShortestTour@t]]]
PathGraph[Range[Length@tour], VertexCoordinates -> t,EdgeShapeFunction -> arrow]

Looks identical to our PathGraph!

Now let's get some shortest paths. For instance the shortest path from vertex 1 to 9:

Overlay[{gg, HighlightGraph[pg, FindShortestPath[pg, 1, 9]]}]

The path is marked with red dots:

---

Algorithmic Graph Theory -- All-Pairs Shortest Path

As usual, when it is about graph theory I'm using the Combinatorica package that comes with Mathematica.

Using the Combinatorica package you could use several shortest path algorithms.

Let's turn your t into a graph. Your weighting function seems to be nothing else, but an EuclideanDistance. In Combinatorica the EuclideanDistance for graphs is defined as Euclidean:

<< Combinatorica`

g = SetEdgeWeights[FromUnorderedPairs[Flatten[t, 1]], WeightingFunction -> Euclidean]
ShowGraph[g, VertexNumber -> True, VertexNumberPosition -> UpperRight]

Let's get the All-Pairs shortest path:

(s = AllPairsShortestPath[g]) // Short

==> {{0,0.618034,<<6>>,1.23607,0.618034},<<8>>,{<<1>>}}

Please have a look at here for further Floyd-Warshall algorithm discussion

Let's get the Euclidean shortest paths from vertex 1 to all other vertices, by producing a shortest-path spanning tree:

t = ShortestPathSpanningTree[g, 1];
ShowGraphArray[{g, t}, VertexNumber -> True, VertexStyle -> Disk[0.05]]

Let's turn this into an ordered graph:

op = ToOrderedPairs[g];
ShowGraph[FromOrderedPairs@op, VertexNumber -> True, VertexNumberPosition -> UpperRight]

Ordered this graph will have a different spanning tree, so let's run again a shortest-path spanning tree:

t = ShortestPathSpanningTree[g, 1];
ShowGraphArray[{g, t}, VertexNumber -> True, VertexStyle -> Disk[0.05]]

Answer 2

Finding the shortest paths between any s and t is usually called the "all-pairs shortest path" problem, as any is generally interpreted as all. You can do that with the JFloyd function in JVMTools. It can compute the all-pairs shortest distances (guaranteed optimal, this is no heuristic) for thousands of nodes in a few seconds, as that page above shows. Unlike the Dijkstra algorithm, which you could in theory call sequentially to solve this, the function JFloyd also accepts negative arc costs (as long as there are no negative cycles in the network).

I would avoid the term "tour" in this context, as it would point towards the TSP, closed or open. Paths are different from tours, and if I understand you correctly (please correct me if I'm wrong), you want the all-pairs shortest path solutions, no tours. If you want an open TSP solution, just solve the TSP and ignore the edge that closes from end back to start.

Disclosure: I am the owner of Lauschke Consulting, which is the business that sells JVMTools commercially.