MoS2 (Transition Metal Dichalcogenide) layer using Mathematica

Question

I'm trying to generate Transition metal dichalcogenide monolayer (MoS2). Can you please assist me with this problem

Thanks and regards

Mo 0.00 0.00 0.1682 S 0.666 0.666 0.2124 S 0.666 0.666 0.12412

Following code I use to generate graphene monolayer. Now I need a monolayer MoS2 system. In graphene all the atoms were in one plane (1 layer). But in MoS2 we have to use z coordinates as well.

(* graphene*)

    `nshell = 30;
     a1 =  {Cos[-30 Degree], Sin[-30 Degree]};
     a2 =  {Cos[30 Degree], Sin[30 Degree]};
     \[Delta] = (a1 + a2)/3;
     L1a = 1. Flatten[
     Table[
      Table[i a1 + j a2 + \[Delta], {j, -nshell, nshell}], {i, - 
      nshell,
      nshell}], 1];
  L1b = 1. Table[i + \[Delta], {i, L1a}];
   ListPlot[{Join[L1a, L1b]}]`

(MoS2) `c1 = 3.16; c2 = (0.242^2) - ((3.16)^2)/3; c3 = 3.5;

     a1 = {c1, 0, 0};
     a2 = {-c1/2, Sqrt[3]/2 c1, 0};
     a3 = {0, 0, 2 c2 + c3};
 \[Delta] = {{c1, 0, 0}, {-c1/2, Sqrt[3]/2 c1, 0}, {0, 0, (2 
  c2 + c3)}};
 ListPlot3D[\[Delta]]`

Thank you very much for the answer.

The lattice may rotate as in this picture starting from (0,0,0) coordinates ( All the coordinates should positive).

What is it you want to do exactly? Generate graphics of the crystal structure? — Sjoerd Smit, Oct 10 '22 at 07:05
On this forum, you have to demonstrate that you tried some steps toward the solution. Please, show your code. — yarchik, Oct 10 '22 at 08:26
So do you want to generate graphics or just the coordinates then? Your answer is unclear. — Szabolcs, Oct 10 '22 at 08:29
I have attached the code I am using for monolayer graphene. I want to make a MoS2 monolayer. — Shen, Oct 11 '22 at 06:07

George Varnavides · Answer 1 · 2022-10-11T17:08:21.550

Edit 01:

The original question asked about a commensurate MoS$_2$ moire. It has since been updated to ask about only the coordinates of an MoS$_2$ monolayer. Considering the answer to the original question might be useful to other people, I'll leave this up. The answer to the updated question only can be found in the second code block.

Original answer

The commensurability of the moire cell is a property of the lattice vectors, not the motif. As such - you can use the following to compute the commensurate angles and commensurate moire cell for two twisted hexagonal lattices (with the same lattice constant):

hexagonalLattice[hexagonalLatticeConstant_] := 
 hexagonalLatticeConstant {{Sqrt[3]/2, 1/2}, {-(Sqrt[3]/2), 1/2}}
commensurateRotationAngle[{m_, n_}] := 
 With[{cos = (n^2 + 4 n m + m^2)/(2 (n^2 + n m + m^2))}, ArcCos[cos]]
commensurateCell[latticeVectors_, {m_,n_}] := {{n,-m}.latticeVectors, {m,n+m}.latticeVectors}

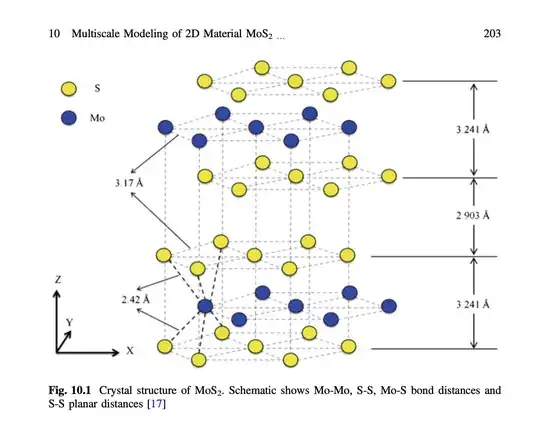
After that, it's a matter of decorating the moire cell with the appropriate honeycomb motif for each layer. Here is an example of a (6,7) commensurate moire cell for twisted bilayer MoS$_2$:

moS2Lattice = ArrayPad[hexagonalLattice[3.19], {{0, 1}, {0, 1}}, 0.];
moS2Lattice[[3, 3]] = 14.879;
distance["Mo-S"] = 1/10;
moS2BilayerMotif = {
   {1/3, 2/3, 1/4}, {2/3, 1/3, 1/4 + distance["Mo-S"]}, {2/3, 1/3, 
    1/4 - distance["Mo-S"]},
   {2/3, 1/3, 3/4}, {1/3, 2/3, 3/4 + distance["Mo-S"]}, {1/3, 2/3, 
    3/4 - distance["Mo-S"]}};

Note I define the full bilayer motif here, the first three coordinates refer to the bottom layer, while the last three to the top layer.

We can visualize this to make sure it looks correct for the untwisted case:

cols = Association[Map[ElementData[#, "AtomicSymbol"] -> ElementData[#, "IconColor"] &, {"Molybdenum", "Sulfur"}]];
moS2Colors = {Darker[cols["Mo"]], Darker[cols["S"]], Darker[cols["S"]], cols["Mo"], cols["S"], cols["S"]};
Graphics3D[
 Thread[{moS2Colors, 
   Sphere /@ (Outer[Plus, moS2BilayerMotif, 
       Tuples[{Range[-3, 3], Range[-3, 3], {0}}], 1] . moS2Lattice)}],
  ViewPoint -> {0, \[Infinity], 0}, Boxed -> False]

Now, we can make two large copies of an untwisted bottom layer and a twisted top layer, and then punch out the atoms inside our moire cell:

moireCellRM = 
  RegionMember[
   Polygon[{{0, 0}, {1, 0}, {1, 1}, {0, 1}} . 
     commensurateCell[moS2Lattice[[;; 2, ;; 2]], {6, 7}]]];
moS2Bottom = 
  Table[Select[atom, 
    moireCellRM[#[[;; 2]]] &], {atom, (Outer[Plus, 
       Take[moS2BilayerMotif, 3], 
       Tuples[{Range[-20, 20], Range[-20, 20], {0}}], 1] . 
      moS2Lattice)}];
moS2Top = 
  Table[Select[atom, 
    moireCellRM[#[[;; 2]]] &], {atom, (Outer[Plus, 
       Drop[moS2BilayerMotif, 3], 
       Tuples[{Range[-20, 20], Range[-20, 20], {0}}], 1] . 
      RotationTransform[commensurateRotationAngle[{6, 7}], {0, 0, 1}][
       moS2Lattice])}];

Let's visualize these to make sure it looks correct:

singleCell = {
   Thread[{Take[moS2Colors, 3], Sphere /@ moS2Bottom}],
   Thread[{Drop[moS2Colors, 3], Sphere /@ moS2Top}]};
twistedMoire = 
 Graphics3D[singleCell, ViewPoint -> {0, 0, [Infinity]}, 
  Boxed -> False, ImageSize -> 350]

and finally tile the plane to make it even clearer:

twistedMoireLarge = Graphics3D[
   Table[
    GeometricTransformation[singleCell, 
     TranslationTransform[{i, j, 1} . 
       ArrayPad[
        commensurateCell[
         moS2Lattice[[;; 2, ;; 2]], {6, 7}], {{0, 1}, {0, 
          1}}]]], {i, -1, 1}, {j, -1, 1}], 
   ViewPoint -> {0, 0, \[Infinity]}, Boxed -> False, 
   ImageSize -> 750] // Rasterize

Thank you very much. I appreciate the informative explanation at each step. This is what exactly what I needed. I have to use this in Lammps molecular dynamics simulation. Can you please print the coordinates and lattice vectors. All the coordinates should be positive. It is better if the structure is starting at (0,0,0) in positive direction. Lattice vectors example: 138.493620415 0.0 0.0 69.246810207 119.938993541 0.0 0.0 0.0 35.0 — Shen, Oct 12 '22 at 02:18

MoS2 (Transition Metal Dichalcogenide) layer using Mathematica

1 Answers1

Edit 01:

Original answer