1

I try to solve an ODE using the trapezoidal method. I do the following (Definition of Trapezoidal is from this answer):

Trapezoidal = {"FixedStep", 
  Method -> {"ImplicitRungeKutta", 
    "Coefficients" -> "ImplicitRungeKuttaLobattoIIIACoefficients", 
    "DifferenceOrder" -> 1, 
    "ImplicitSolver" -> {"FixedPoint", 
      AccuracyGoal -> MachinePrecision, PrecisionGoal -> MachinePrecision, 
      "IterationSafetyFactor" -> 1}}};

y = t /. First@NDSolve[{y'[t]  ==Sin[t]-2y[t], y[0] == 0}, y, {t, 0, 20}, 
  Method -> Trapezoidal, StartingStepSize -> 1/100];
Plot[y[t], {t, 0, 20}]

But I get a warning message:

NDSolve`ImplicitRungeKutta::cmsing: Singular coefficient matrix encountered for NDSolve`ImplicitRungeKuttaLobattoIIIACoefficients, which is not suitable for stiff systems.

Then I try to plot these points resulting from the procedure as a path, but still can't get that working.

Any idea how I can make this work?

Thanks.

xzczd
  • 65,995
  • 9
  • 163
  • 468
Vangsnes
  • 591
  • 2
  • 9

1 Answers1

3

Let me extend my comments to an answer. First of all,

Then I try to plot these points resulting from the procedure as a path, but still can't get that working.

As mentioned above, this is because you're using ReplaceAll (/.) blindly, /. just doesn't have the functionality you're imagining. Here I'll simply show the fix without explanation:

ysol = y /. First@
    NDSolve[{y'[t] == Sin[t] - 2 y[t], y[0] == 0}, y, {t, 0, 20}, 
     Method -> Trapezoidal, StartingStepSize -> 1/5];

ListPlot[Transpose@{ysol["Coordinates"][[1]], ysol["ValuesOnGrid"]}]

enter image description here

Please read document of ReplaceAll (/.), this and this post and the document Utility Packages for Numerical Differential Equation Solving to understand why the points are extracted in this manner.

Remark

A less advanced solution is

ListPlot@Table[{t, ysol[t]}, {t, 0, 20, 1/5}]

Notice this method doesn't extract the original data so if you compare the data with that obtained above, you'll observe extremely small discrepency, but this should be trivial for any pedagogical purpose programming.

OK, then let's talk about the interesting part of this question:

I get a warning message NDSolve`ImplicitRungeKutta::cmsing…

Conclusion first: this is merely a warning, NDSolve still uses the trapezoid rule for ODE solving, so you can simply ignore it.

Why do I know it can be ignored? Because after some spelunking using the debugger tool (you may start from this post to learn the usage of debugger), I notice the warning is caused by an internal function NDSolve`IRKDump`InvertWeights, its definition is

Internal`$ContextMarks = False;
?NDSolve`IRKDump`InvertWeights

enter image description here

As we can see, when the method NDSolve`ImplicitRungeKuttaLobattoIIIACoefficients is set, NDSolve`IRKDump`InvertWeights always returns $Failed. I'm not familiar with implicit Runge-Kutta method so cannot comment on this design. I just want to point out that, if the first definition is cleared, and undocumented option Method -> "IterativeRefinement" is not set in LinearSolve, InvertWeights will be able to find the invert weights:

(* You need to use Method -> "ImplicitRungeKutta" at least once
   before executing the following code *)
NDSolve`IRKDump`InvertWeights[
  NDSolve`ImplicitRungeKuttaLobattoIIIACoefficients, __] =.

NDSolveIRKDumpInvertWeights[method_, {amat_, bvec_, cvec_}, prec_] := 
 Module[{dvec}, Block[{Message}, dvec = LinearSolve[Transpose[amat], bvec];]; 
  If[! NDSolveIRKDumpNumberVectorQ[dvec], $Failed, dvec]]
(* {0., 1.} *)

After executing the code above, you'll find the warning NDSolve`ImplicitRungeKutta::cmsing no longer shows up. I'm not sure if it's safe to modify code like this, the obtained solution remains the same anyway.

"But wait, how do you know the trapezoid rule is really used internally? Perhaps NDSolve has turned to something else! " This can be easily verified by comparing the result to a home-made trapezoid rule solver:

t0 = 0; tend = 5; dt = 1/2; y0 = 0;
rhsfunc = {t, y} |-> Sin[t] - 2 y;
sys = {y'[t] == rhsfunc[t, y[t]], y[t0] == y0};
asol = y /. First@DSolve[sys, y, {t}]
nsol = NDSolveValue[sys, y, {t, t0, tend}, 
   Method -> {FixedStep, 
     Method -> {ImplicitRungeKutta, 
       Coefficients -> ImplicitRungeKuttaLobattoIIIACoefficients, 
       DifferenceOrder -> 1}}, StartingStepSize -> dt];

onestep = With[{f = rhsfunc}, 
   Compile[{t, y0, dt}, 
    Last@FixedPoint[
      Function[{ylst}, 
       Module[{k1, k2}, 
        k1 = f[t, ylst[[1]]]; 
        k2 = f[dt + t, ylst[[2]]]; 
        {ylst[[1]], 1/2 dt (k1 + k2) + ylst[[1]]}]], 
        {y0, y0}, SameTest -> (Abs[#1[[2]] - #2[[2]]] < 1*^-10 &)]]];
tlst = Range[t0, tend, dt];
datatrapezoid = FoldList[onestep[#2, #, dt] &, 0, Most@tlst];
datansol = nsol["ValuesOnGrid"];
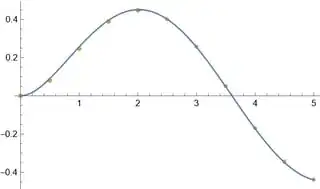
ListPlot[{datatrapezoid, datansol}, DataRange -> {t0, tend}]~Show~
 Plot[asol[t], {t, t0, tend}]

enter image description here

(* Error Check *)
asol@tlst - # & /@ {datansol, datatrapezoid} // 
 ListPlot[#, PlotMarkers -> {"X", "O"}, DataRange -> {t0, tend}] &

enter image description here

As we can see, the numeric error of NDSolve solution and home-made solver solution consistents, so it's reasonable to believe the trapezoid rule is indeed used by NDSolve.

xzczd
  • 65,995
  • 9
  • 163
  • 468