0

I have an equation that seems very simple. I want to find the root of the equation. NSolve can not solve this equation, because it says "This system cannot be solved with the methods available to NSolve". That is why I use the FindRoot command. However, FindRoot does not give me trustable results. Depending on the initial points, it gives different results. I think this is related to the error it gives me which is "General::ovfl". When I plot the function, it looks straightforward, and I expect Mathematica to solve it quickly, but it doesn't solve it. Here is the simplified version of my equation:

FindRoot[10^(-71)*(2-Gamma[3,10^33 x])/x^2==10^-6,{x,10^-34,100}]

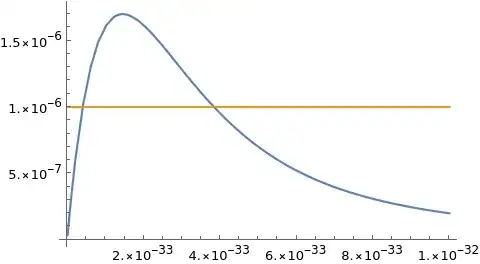
Here is the plot of the two sides of the equation

enter image description here

As you see, the roots are around 3 10^-34 and 3.8 10^-33. I can get these results by changing the initial points. But, the question is why the result is very dependent on the initial points. Also, in many initial points which are still reasonable points, Mathematica does not give any of the correct roots. I guess the problem is related to the Overflow error.

The real problem I am dealing with is more complicated than this, and I have to find the root of many points. So, I can not change the initial point for each point.

So, my question is how can I find the root of this equation?

I will be very thankful if someone helps me.

Mehrdad
  • 111
  • 6
  • how about then writing FindRoot[ 10^(-71)*(2 - Gamma[3, 10^33 x])/x^2 == 10^-6, {x, 3*10^-34, 3.8 *10^-33}]? This gives {x -> 4.07892*10^-34} with no warning of overflow. The smaller the range of the search, the better the chance you will not see the overflow Mathematica graphics in V 13.1 I think there is a package which will do better job finding all roots in a range and not just one. If you search this forum for this topic you will find it... – Nasser Nov 19 '22 at 20:01
  • ... see find-all-roots-in-range for example – Nasser Nov 19 '22 at 20:05
  • Thank you Nasser for your comment. As you noticed, changing the range a bit changes the result dramatically. Let's say choosing the range {x, 10^-34, 10^-30}does not give any of the roots. The reason that I am changing the range is that in the problem I am working I do not know the possible value of the root. I only know it should be in the range {x, 10^-40, 10^-28} – Mehrdad Dec 01 '22 at 02:27

2 Answers2

3

FindRoot will only return a single solution. The initial starting point is needed to point it at a particular solution. You can map FindRoot onto a list of starting values. For this particular problem, a relatively high WorkingPrecision is required.

eqn = 10^(-71)*(2 - Gamma[3, 10^33 x])/x^2 == 10^-6;

(sol = FindRoot[eqn, {x, #},
      WorkingPrecision -> 45] & /@ {3^-34, 38^-34}) // N


(* {{x -> 4.0528910^-34}, {x -> 3.8409910^-33}} *)


eqn /. N[sol]


(* {True, True} *)

EDIT: Using NSolve

(sol2 = NSolve[
    {eqn, 4*^-34 < x < 4*^-33}, x,
    WorkingPrecision -> 45]) // N

(* {{x -> 4.0528910^-34}, {x -> 3.8409910^-33}} *)
Bob Hanlon
  • 157,611
  • 7
  • 77
  • 198
  • Thank you for your reply. Your solution is amazing. The first method is working pretty well. I change the range and still gives me the correct solutions. However, I am not familiar with the commands you are using. Can you say more about what you mean by {x,#} and & /@? Is there any way to write the commands in a more traditional way that beginner people such as me know it :)? The second method does not work for a broader range. So, I just focus on the first way. – Mehrdad Dec 01 '22 at 02:43
  • Looka the documentation for Function and Map – Bob Hanlon Dec 01 '22 at 04:37
3

Here is an alternative approach using only machine precision. We want to find a root of

f[x_] := 10^(-71)*(2-Gamma[3,10^33 x])/x^2-10^-6;

From inspection of the expression, or from OP's plot, we know that typical interesting input values are on a scale $\approx 10^{-33}$. On the other hand, a numerical function such as FindRoot or its default settings sometimes prefer a scale $\approx 1$. So one approach is to simply change the scale, and this works:

With[{scale=10^(-33)},
   scale*x /. FindRoot[f[scale*x],{x,1}]]
(* 4.05289*10^-34 *)

Similarly

With[{scale=10^(-33)},
   scale*x /. FindRoot[f[scale*x],{x,4}]]
(* 3.84099*10^-33 *)
user293787
  • 11,833
  • 10
  • 28