I have some data of the form {{x1, y1}, {x2, y2}, ..., {xn, yn}}. It is already sorted by x values. I am looking for a simple way to resample it and obtain {{rx1, ry1}, {rx2, ry2}, ...} for a given set of {rx1, rx2, ...} coordinates, in such a way that the ry value corresponding to an rx will be the same as the y value of the nearest left x neighbour of rx.
Suppose the data is
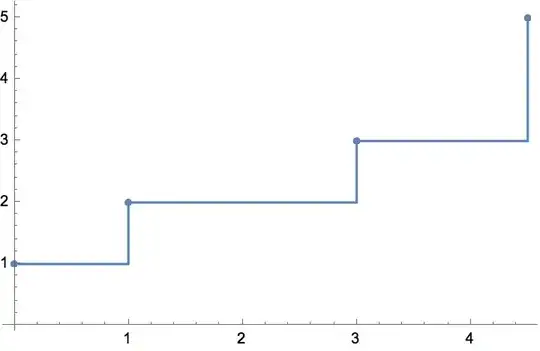
data={{0, 1}, {1, 2}, {3, 3}, {4.5, 5}}
Then I am basically looking to take values from the function plotted below, for an arbitrary set of x values:
ListPlot[{{0, 1}, {1, 2}, {3, 3}, {4.5, 5}}, InterpolationOrder -> 0,
Joined -> True, PlotMarkers -> Automatic]
Is there anything built in for this?
Plot[Interpolation[{-#, #2} & @@@ InterpolationOrder -> 0][-x], {x, 0, 4.6}, PlotRange -> {0, 5}]– Lukas Lang Nov 22 '22 at 23:04Nearest(i.e. a binary search for each point) feels like a huge overkill ... – Szabolcs Nov 30 '22 at 14:35Fold*variants, but those quickly become unreadable. – Lukas Lang Nov 30 '22 at 21:47