Tangents of 2 circles

Question

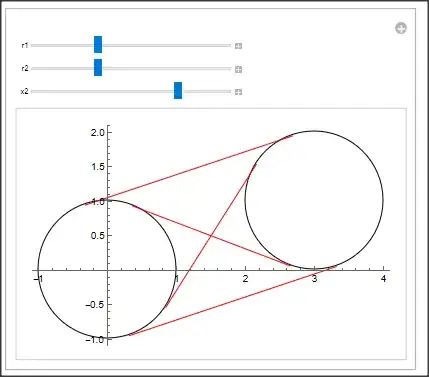
I am trying to write a function, tanCircles[], that finds the common tangents to two given circles (one not inside the other). The function's parameters are two list, each containing the x and y coordinates of the center and the radius. If one circle is inside the other, the function should return an error message. Otherwise, the function should return the equations of all tangents found. This is what I have tried but doesn't seem to be right.

Block[{t1, t2, v1, v2, pts}, t1 = {xm, ym};
 t2 = {xn, yn};
 {v1, v2} = p[];
 pts = {t1, t2} /. 
   NSolve[{(t2 - v2) . (t2 - t1) == 0, (t1 - v1) . (t2 - t1) == 
      0, (t1 - v1) . (t1 - v1) == r1^2, (t2 - v2) . (t2 - v2) == 
      r2^2, (t1 - v1) . (t2 - v2) > 0}, {xm, ym, xn, yn}, Reals];

if the circles are disjoint, do you want four tangents? – lericr Nov 25 '22 at 21:08 — lericr, Nov 25 '22 at 21:08

score 1 · Accepted Answer · answered Nov 25 '22 at 22:13

Name c1 and c2 the centers of the 2 circles and r1, r2 their radii. Call p1 and p2 the tangent points on the 2 circles. Then you can write the following equations:

eq = {(p1 - c1) . (p1 - c1) == r1^2, (p2 - c2) . (p2 - c2) == 
   r2^2, (p1 - c1) . (p1 - p2) == 0, (p2 - c2) . (p1 - p2) == 0}

Solving these equations gives you the tangent points.

Here is a simple application:

fun[{c1_, r1_}, {c2_, r2_}] := 
 Module[{p1 = {px1, py1}, p2 = {px2, py2}},
  eq = {(p1 - c1) . (p1 - c1) == r1^2, (p2 - c2) . (p2 - c2) == 
     r2^2, (p1 - c1) . (p1 - p2) == 0, (p2 - c2) . (p1 - p2) == 0};
  sol = {p1, p2} /. Solve[eq, Flatten@{p1, p2}] // Quiet;
  sol = Cases[sol, x_ /; FreeQ[x, Complex[_, _]] && FreeQ[x, py1], 1]
  ]
Manipulate[
 sol = fun[{{0, 0}, r1}, {{x2, 1}, r2}]; Print[sol[[1]] // Simplify];
 Graphics[{Circle[{0, 0}, r1], Circle[{x2, 1}, r2], Red, Line[sol]}, 
  Axes -> True]
 , {{r1, 1}, 0.5, 2}, {{r2, 1}, 0.5, 2}, {{x2, 3}, 0, 4}, 
 TrackedSymbols :> {r1, r2, x2}]

Tangents of 2 circles

1 Answers1